【摘要】:Maag首先推导出浆液在砂层中的渗透公式,它至今仍被广泛采用。在推导公式时,Maag作了下述一些简化计算模式的假定:被注砂土为均质和各向同性的。浆液在地层中呈球状扩散。图2.4底端注浆球形扩散图浆液扩散的理论模型如图2.4所示。Maag公式比较简单,对粘度随时间变化不大的浆液能给出渗入性的初步轮廓。表2.1浆液的扩散半径表中数字大体说明,该浆液用于中砂是比较适宜的。
Maag(1938年)首先推导出浆液在砂层中的渗透公式,它至今仍被广泛采用。在推导公式时,Maag作了下述一些简化计算模式的假定:
(1)被注砂土为均质和各向同性的。
(2)浆液为牛顿体。
(3)采用填压法注浆,浆液从注浆管底端注入地层。
(4)浆液在地层中呈球状扩散。
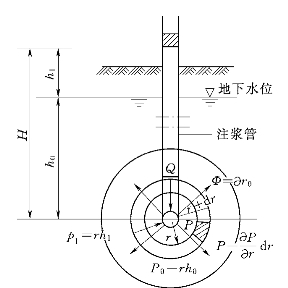
图2.4 底端注浆球形扩散图
浆液扩散的理论模型如图2.4所示。h0为注浆点以上地下水压头;H为地下水压头和注浆压力水头之和(cm);该理论的注浆时间t和浆液扩散半径r1表达式如下:
![]()

式中 k——砂土的渗透系数,cm/s;
β——浆液粘度对水的粘度比;
h1——注浆压力水头,cm;(https://www.daowen.com)
r0——注浆管半径,cm;
n——砂土的孔隙率。
Maag公式比较简单,对粘度随时间变化不大的浆液能给出渗入性的初步轮廓。例如用某种硅酸盐浆液注浆,当注浆压力为70m水头,注浆管半径为2.5cm,土的孔隙率为0.3,浆液粘度对水的粘度比等于3,浆液凝结时间为35分钟时,试验证明在20分钟内浆液的粘度基本上不变,则灌注20分钟后浆液在各种土中的渗入半径见表2.1。
表2.1 浆液的扩散半径

表中数字大体说明,该浆液用于中砂是比较适宜的。
除Maag公式外,常见的还有Karol和Raffle公式:
Karol公式
![]()

Raffle公式
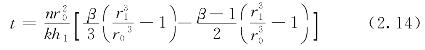
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章







