列几个DFT/IDFT常用性质，大多数和（连续）傅里叶变换性质类似，我们只选其中部分证明，其他请大家自己动手（查资料或自己推导等）搞定。

（1）时域循环移位，频域相位旋转

为了更直观，我们假设N=3，m=1来演示证明过程，不然DFT矩阵太大表示不清楚。

DFT{x[（n-m）mod N]

（2）时域相位旋转，频域循环移位

（3）时域循环卷积，频域乘积（1）

其中，运算

表示两个序列x₁（n）和x₂（n）的循环卷积，也记为。

证明 同样为了更直观，我们假设N=3来演示证明过程。首先，采用矩阵形式，

那么有，

注意到，上面式子中，中间那个矩阵的每一列实际上是序列x₁（n）的不同循环移位，从而根据“时域循环移位，频域相位旋转”性质知，DFT矩阵（上面式子中第一个矩阵）作用于其中每一列得到的是X₁（n）的不同相位旋转，即上面式子等于

仔细观察知，

代入继续看到，后两个结合又是一个标准的DFT变换，则继续化简为

证明完毕。

大家可以看到，证明过程中主要是多注意观察，灵活分拆与组合矩阵形式，大家多练习，熟能生巧，那把剩下的留给大家啦！

（4）时域循环卷积，频域乘积（2）

（5）时域循环卷积，频域乘积（3）

（6）时域乘积，频域循环卷积

（7）斜对称

X（n）～Nx[（-n）mod N]（C-87）

（8）共轭斜对称(www.daowen.com)

x（n）*～X[（-n）mod N]*（C-88）

（9）时频能量守恒

上面所有的性质都是假设涉及的序列在复数域上成立的，而如果某个序列的所有数都是实数，还有一些额外的特殊性质，下面仅列举一个，其他的请大家根据实数的一些特殊性来自己思考。

性质C-16 如果序列x（n），n=0，…，N-1为实数序列，那么

X（n）=X*[（-n）mod N]（C-90）

证明 首先，“共轭斜对称”性质是对所有复数域上序列都成立的，即

x*（n）～X*[（-n）mod N]

当然实数序列也不例外。但是，另一方面，对于实数序列有

x*（n）=x（n）

所以，它们各自的DFT后序列也相等，则

X*[（-n）mod N]=X[n]

性质C-17 记DFT矩阵为[DFT]。显然，可以证明DFT变换是线性变换，即有

X₁+X₂=[DFT]x₁+[DFT]x₂=[DFT][x₁+x₂]（C-91）

还可以证明知

[DFT][DFT]^H=diag{N，…，N}（C-92）

其中，diag{…}为对角阵。更进一步知，归一化后的DFT矩阵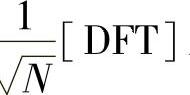为酉阵（复数域上的正交矩阵），即

从而，若两个序列x=[x₀，…，x_N-1]和序列y=[y₀，…，y_N-1]在时域正交，那么它们对应的频域序列[DFT]x和[DFT]y也是正交的。

逆变换IDFT及对应的矩阵也和DFT及对应矩阵有同样的性质，大家可以自己写一下。

练习C-5在频域奇数位上放序列X_n，n=0，…，N，偶数位为0，或者相反。请问做2N点IDFT后，时域出来的点有什么特征？并请推广。（提示：答案是某种序列的重复。）