对长度为N的离散序列f_n对应的傅里叶变换进行采样，采样点个数N_c，这N_c个点为

下面分三种情形讨论什么时候序列f_n与F_n有一一对应关系。

1.情形一：N_c<N

注意当n≥N_c时，

那就是说，当n≥N_c时，f_n与f_n-Nc可以先合并成一项，即

所以，如果序列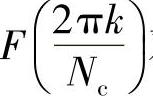对应序列f_k，那么序列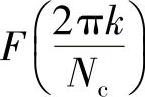必然也对应任何序列f_k＇。其中，当n≥N_c时，有

f_n+f_n-Nc=f_n＇+f_n＇-_Nc

对于其他N-N_c≤n<N_c，f_n=f_n＇。或者，等价地描述为，当0≤n≤N-N_c-1时，有

f_n+f_n+Nc=f_n＇+f_n＇+N_c

对于其他N-N_c≤n<N_c，f_n=f_n＇。因此，情形一不可能有一一对应关系。

2.情形二：N=N_c这次没有合并的情况，从序列整体上看，得到的采样点序列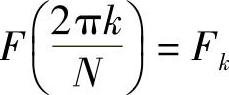可以看成f_n与N个序列线性组合而来，这N个序列是原来连续基信号序列分别采样得到的序列，即

如果这N个序列正交就好了，那我们就一定知道F_n只能唯一地由f_n得到。运气真好，它们确实是正交的。在证明之前，我们先介绍一个代数基本定理：(www.daowen.com)

定理C-15（N次单位根）方程x^N=1的N个根为

并且

证明 先根据多项式分解有

当x≠1时，必然有1+x+x²+…+x^N-1=0。即取值非1的根的各幂次之和为0，得证。

现在证明上面的序列正交，其两个不同序列内积为

从而，情形二可以建立一一对应关系。

3.情形三：N_c>N

采样得到的N_c个点可以写成

当写成这种形式，它其实就是情形二了。根据情形二的讨论，我们知道序列f_n＇和序列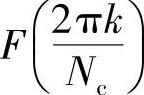一一对应，其中

注意，序列f_n＇后半截全是固定的0，前半截完全等于f_n，那么唯一确定了序列f_n＇自然就确定了序列f_n了。所以，情形三也是能一一对应的。

把上面的讨论进行归纳，就可以得到DFT/IDFT理论了。