线性空间知识在前面的傅里叶级数和傅里叶变换等推导中，似乎是万能灵药一样，所向披靡啊。不知对于采样定理还灵不灵？嘿，你别说，只要会用，一样能制服采样定理。下面，大家一起来看看。

假设F（ω）为角频率区间-W/2≤ω≤W/2上的信号（可以是“虚拟”频谱区间），记

f（t）=-1{F（ω）}不妨设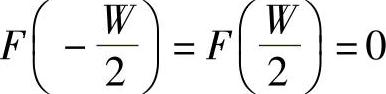。根据性质2-4，那它可以由正交基

来表示，其中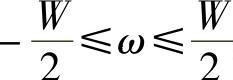。或者，等价写成正交基

首先根据坐标计算方法，把信号F（ω）在该组基下的坐标写出来为

注意到，上面坐标表达式的分子其实是F（ω）的傅里叶变换（仅仅是把常用的自变量t换成了ω）在某个点的值（当然，你也可以看成傅里叶逆变换的某个值）。记

那么，坐标表达式（C-62）的分子等于(www.daowen.com)

然而，根据傅里叶变换的“斜对称”性质，又可以得到

则，最后得到信号F（ω）在该组基下的坐标为

那么，我们看到F（ω）居然能由f（t）的一系列离散点的值和一组基线性组合表示出来，离散点可以看成是通过采样得到的，看来有戏：

变换到时域信号f（t），则

记2π/W=T，则

可以看到，信号f（t）能由其上等间隔点f（n子）与一组和f（t）无关的信号联合重构出来，这就是采样定理的实质。似乎成功了？确实成功了！可以看到，我们从线性空间理论照样可以推导出采样定理，关键还是多观察、多思考，总是能有所收获。