性质C-7（信号积分）信号f（t）的积分

证明 观察知

另一个类似，证明完毕。

这性质很有意思，其实前面傅里叶级数也有类似性质，只是没提，大家可以再返回去想想傅里叶级数对应于这个的性质应该是什么样的，留做练习。

性质C-8（能量守恒）同一能量信号的时域表示和频域表示，信号能量守恒，即

证明 首先还是假设f（t）是т≤t≤т+T₀上信号，其中T₀→∞。它可以由正交基

来表示，其中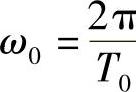，ω0→0。由第一部分2.2节里傅里叶变换的推导知，f（t）在基

e^jωt，ω=nω₀，子≤t≤子+T₀

下的坐标为

而基信号的模（也就是能量）为

根据线性空间里向量模与坐标的关系，有

当ω₀→0时，上式等于

线频率f的情形推导类似，故得证。

可以看到，能量守恒可以看成模与坐标关系的简单应用，也即还是线性空间理论的简单应用，但它有个专门名称叫帕斯瓦定理（Parseval’stheorem）。

除了上面几个性质，傅里叶变换还有很多特殊的性质，以及特殊的变换对，基本上都可以根据傅里叶变换定义公式变形得到。这里只给出常用的。另外，部分性质举例了一些技巧推导，剩下的大家也可以自己练习，关键是观察，灵活应用。

（1）复指数函数的傅里叶变换

e^jω₀t～2πδ（ω-ω₀）（C-39）

回忆傅里叶变换实质是求e^jωt基下坐标，信号e^jω0^t已经是这种形式了，就不用多此一举了。也就是说复指数信号e^jω0^t在其他基e^jωt，ω≠ω₀下的坐标为0，即

F（ω）=0，ω≠ω₀

而在基e^jω0^t下的坐标为1，即

从而

上面用到式（1-5）所示性质δ（0）=1

dω，前面讲冲激信号性质时讲过，请回忆或复习一下。再由傅里叶变换F（ω）的积分

那么，和冲激信号定义1-3对比知，F（ω）为在ω=ω₀的一个幅度为2π的冲激，即

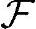{e^jω0^t}=2πδ（ω-ω₀）

当然，也可以直接根据傅里叶变换的定义，计算积分试试。

（2）时域平移，频域相位旋转

从公式计算上理解：

从向量空间理解：一般讨论向量时，我们都假设向量是从原点出发的。但实际中，平移到其他点出发后的向量仍然是实质等价的一个向量。现在问题变成，这些平移后的向量在原来确定的基下坐标怎样？

这样想，如果基也跟着平移t→t-t₀的话，坐标在平移后的基下肯定不会发生变化，即平移前有

平移后必然有

图C-4 向量及基平移

但是，我们现在想要的是在原基下的坐标，即不允许基也跟着平移，那把上式写成原来基e^jωt的形式看看

可以看到，在原来基下坐标为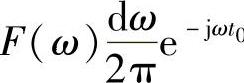，即

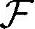{f（t-t₀）}=F（ω）e^-jωt0

思考一下，这个性质的意义在哪儿？因为对于单个信号来说，无所谓时域平移不平移，因为你可以调整坐标。那就是说，当我们把时域坐标调整后，所谓的频域相位旋转又没了，那也就是说频域相位这个东西是可有可无的，是这样吗？暂时不公布答案。

这一条，还可以让我们看到，频域是绝对坐标，不是想调整就可以调整的，频点是多少就是多少。不同时刻发生的信号f（t）和f（t-子）本质应该是一样的，所以一定有某样东西是不变的，它们对应的频域自变量范围就反映了这一“不变”的东西。

（3）时域旋转，频域平移

可以像上面性质（2）同样的角度讨论，略。

（4）伸缩变换(www.daowen.com)

（5）时频斜对称

F（t）～2πf（-ω）（C-43）

（6）时域卷积，频域乘积

∫f₁（子）f₂（t-子）d子～F₁（ω）F₂（ω）（C-44）

（7）时域乘积，频域卷积

直接用定义进行变换证明：

（8）冲激信号与常数变换对

δ（t）～1

1～2πδ（ω）（C-46）

从公式计算上理解

我们知道任何信号f（t）总是可以写成和冲激信号δ（t）卷积的形式，那么从“时域卷积，频域乘积”性质看，有

故，必然有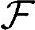{δ（t）}=1。

（9）正弦和余弦

利用正余弦的指数表示

再利用性质（1）可得。

（10）n阶微分 如果信号f（t）的n阶微分f（n）（t）存在，那么

f（n）（t）～（jω）nF（ω）（C-48）

证明很简单，因为

图C-5 正余弦傅里叶变换频谱

则

比较傅里叶变换定义得证。这个性质很有意思，结合线性时不变系统的知识，如果一个线性系统的传递函数为jω，那么一个可微分信号输入该系统后，输出信号就是该信号的微分。这样一个线性时不变系统也可以称为微分系统。

讲了这么多性质，举几个简单例子应用一下吧。

练习C-2 假设信号f（t）的傅里叶变换为F（ω），请计算信号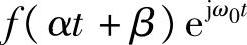的傅里叶变换？如果还不太熟练，我们一步一步来：首先，将信号f（t）自变量伸缩变换到信号f（αt），由“伸缩变换”性质知

再将信号f（αt）的自变量向左平移β/α得到信号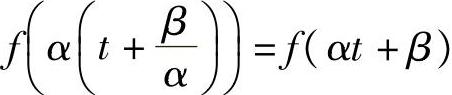，由“时域平移，频域旋转”性质知

最后，再将信号f（αt+β）进行相位旋转e^jω0^t得信号f（αt+β）e^jω0^t，由“时域相位旋转，频域平移”性质知

总之，一个复杂的信号可以由一个简单信号一步步变换过来，在应用傅里叶变换性质的时候也可以分解为一个个的应用最后组合在一起。

练习C-3 我们在本章的最开始就说了，表示论的一个目的是把同一个问题以不同的形式表示出来，有时候在某些表示形式下更容易求解，比如下面这个例子：

求解满足微分方程的信号f（t），

如果我们在微分方程等式两边同时取傅里叶变换，可以得到

从这个方程，我们可以求得

要想得到f（t），对F（ω）求傅里叶逆变换就好了。可以看到，一般来说微分方程是比较复杂一点的，但如果我们应用一下傅里叶变换，就可以把微分方程变成只含加减乘除的代数方程，大多数时候求解简单得多。

性质C-9（轮转性质）一个信号的傅里叶逆变换，与该信号的傅里叶变换关于自变量镜面对称，仅差一个函数值缩放系数，即

证明 联合应用

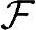{f（t）}=F（ω）和{F（ω）}=2πf（-t）知

观察比较可证。

注意，上面等式中自变量ω、t写成那样，只是为了符合习惯，把频域信号（被计算傅里叶逆变换的信号）的自变量写成ω，而时域自变量记为t而已。大家应用时，不要被这个记号所捆饶哈。比如，我们还也可以把该性质写成

轮转性质其实是“时频斜对称”性质的一个变形，虽然容易推导出来，但是挺有用的。为什么呢？因为一般人习惯正向记忆和计算傅里叶变换，但偶尔要计算逆傅里叶变换时，觉得不习惯。上面的性质可以照顾你的习惯，让你继续正向计算傅里叶变换，最后加个简单变换就得到逆傅里叶变换了。要不大家试试下面这个例子，体会一下。

练习C-4 假设信号f（t）的傅里叶变换为F（ω），请计算信号f（αt+β）e^jω0^t的傅里叶逆变换。同时对于傅里叶变换的每一个性质，应用该轮转性质，可以方便地写出其对应的傅里叶逆变换形式，具体地请大家动手写一写吧。