这一节讨论第一部分里省略的关于傅里叶级数的数理推导与知识扩展。

性质C-5 函数组

{1，cos（ω₁t），sin（ω₁t），…，cos（nω₁t），sin（nω₁t），…}，-∞<t<∞（C-21）在函数的常规内积下是一组正交向量组，且构成“所有”周期为T₁/k或角频率为kω₁的实周期函数组成的线性空间的一组正交基，其中k>0为整数。且有

所以，如果周期信号f（t）的傅里叶级数展开存在，根据正交基下坐标计算方法，我们有

性质C-6（实信号频率幅度对称性）如果f（t）是实信号，那么

F（nω₁）*=F（-nω₁）（C-28）

F（nω₁）=F（-nω₁）（C-29）

即幅度是关于正负频率对称的。

证明 如果f（t）是实信号，那么f（t）=f（t）*，必然得到

从而

F（nω₁）=F（-nω₁）

练习C-1 相对于性质2-4，令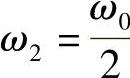，T2=2T₀。显然，复指数函数集合

也是一组正交向量组，且构成“所有”周期为T₂/k或频率为kω₂的复周期函数组成的线性空间的一组正交基，其中k>0为整数。显然，如果信号f（t）是周期为T₀的信号f（t）=f（t+T₀），它也可以看成周期为T₂的信号f（t）=f（t+T₂）=f（t+2T₀）。也就是说，信号f（t）也可以由该组基线性表示。但是，我们已经知道，信号f（t）可以由性质2-4里的复指数函数集合唯一线性表示。且另外注意到，性质2-4里的复指数函数集合是上面这个函数集合的子集，因为

那么，由(www.daowen.com)

可知f（t）已经可以写成{…，e^jnω2^t，…}这个函数集合的线性组合了，且观察到在基e ^j（2m+1）ω2^t下的坐标为0；然而，根据正交基的特性，如果能由某个正交基表示，必然坐标唯一。那怎么从其他方面证明在基e^j（2m+1）ω2^t下的坐标为0呢？提醒，也许会用到下面这个小性质：

这个小性质的证明也留做练习吧。

知识扩展 数学大师陈省身大师说，表达式

eⁱπ=-1（C-31）

很优美，包含了所有特别的数e、i、π、1。那么，为什么会有虚数/复数呢？

数学家，特别是代数学家，总是希望把自然界所有研究的东西都用像“数”的东西来刻画，然后再在其上定义运算规则，最后所有问题都变成运算。解析几何就是这样一个应用之一。既然通常的一维数——实数，能够有简单的加减乘除运算、交换律、结合律、逆元等，那么，如果要同时处理两个数（两个参量），即二维数组，可不可以也有这么简单且实用的运算呢？首先，把二维数的第二维数做个标记i，并且整体表示成x+iy的形式，其他所有的运算形式上都和包含两个项的多项式一样，还要求最后的结果只能是x+iy的形式，不能有i²，那现在唯一的工作就是确定i²。

现在要求任何非0+i0的二维数，一定存在另一个非0+i0的二维数和它相乘等于1（即存在乘法逆元），会发现i²=-1刚好可行。这样，二维数就有了像一元数一样的所有简单运算，也就变得有实际意义了。

接下来，任何一维数的函数扩展成二维数的函数，那么有e^iz，像一元数一样Taylor展开得

其中的偶数次幂刚好是cosz的展开，奇数次幂提出i刚好是sinz的展开，从而有Euler公式

e^iz=cosz+isinz

后续，其他人继续考虑把维数增加还能不能保持现在这样的性质，答案貌似否定的。比如，哈密尔顿（Hamilton）考虑了四元组，形如x+iy+jz+kw，差不多有这样的性质，但是乘法不满足交换律。

另外，值得一提的是，虽然把i这个虚数标记加进来，并定义它参与运算的规则，能理论上使得复数构成一个数域，使得理论运算分析处理简便，但现实中复数还是得由一个一个实数生成。