信号之间的加减乘除运算，就是函数相应的运算，相信不必多介绍了。下面先简单回顾一下信号的平移变换和伸缩变换，这两个都可以看成信号的一元运算，再主要介绍大家可能不那么熟悉的两类二元运算——相关运算和卷积运算。

1.平移变换

信号f（t），其中t₀<t<t₁，在参考坐标轴不变的情况下，向右平移时间 т 得到的信号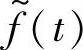，其中t₀+т<t<t₁+т，有没有可能用f信号表示信号呢？怎么实现呢？

首先什么叫表示一个信号？无非是确定信号的自变量范围和相应函数取值。而信号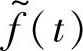的自变量取值区间已经明确知道是t₀+т<t<t₁+т，需要确定的只有该区间上每个自变量点对应的函数值。注意到，因为是平移，函数值整体上并没有改变。对于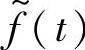每一个自变量t，其对应的函数值是f（t）在t-т 点对应的函数值平移过去的，所以对任意一个t，有

也就是说，f（t）向右平移 т 后得到的信号为f（t-т）。

反过来看，对于f（t-т）要有意义，括号里面的自变量表达式需要满足

图C-1 信号的平移变换

这也隐含了信号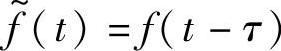的自变量t的取值范围为t₀+т<t<t₁+т。也就是说，信号f（t-т）既表示了信号f～（t）的自变量范围，也表示了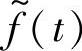在该范围相应的函数值。从而，用信号f完全表示了f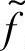。另外，当т<0时，其实是向左平移，不再单独描述了。

2.伸缩变换

关于信号的伸缩变换，可以分为两种：一种是整个自变量范围内所有点对应的函数值都被放大或缩小；一种是自变量取值范围被压缩，但对应函数值不变。一般更多地是指第二种，当然两种可以同时存在。

第一种很简单，信号f（t）函数值被放大a倍得到的信号为af（t），自变量范围不变。当然a<1时，实际是缩小。

第二种稍微复杂点，信号f（t），其中t₀<t<t₁，自变量被压缩a倍，即是使得得到的信号f～（t）的自变量范围为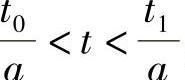，但对应函数值不变。例如，t₀+т被压缩成了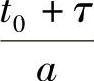，它们的函数值应该相等，即

从而，一般情况有

和上面平移变换类似，要使得f（at）有意义，括号里面的表达式满足

t₀<at<t₁

即信号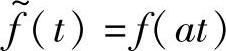隐含了自变量t的取值范围为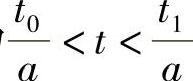。最后，信号bf（at）表示由f（t）自变量范围被压缩a倍，同时函数值放大b倍得到的信号，其函数曲线变化如图C-2所示。

图C-2 信号的缩放变换

3.相关运算

给定两个信号f₁（t）和f₂（t），怎么刻画f₁（t）与f₂（t）的线性相似度呢？或者怎么求f₁（t）的基于f₂（t）的平方误差最小的线性近似，即求C使得下式最小：

在讲解如何求C之前，我们先补充点数学知识。

定义C-1（极值点）对于实函数f（t），如果存在一个区间（不论大小），在该区间内，如果某个点的函数值比它周围点的函数值都大或都小，那么该点称为f（t）的一个极值点。比周围都大的点为极大值点；比周围都小的点为极小值点。

定义C-2（最值点）对于实函数f（t），在一个区间内，如果某个点的函数值比该区间内其他点的函数值都大或都小，那么该点称为f（t）在该区间的一个最值点。比其他点都大的点为最大值点；比其他点都小的点为最小值点。

显然，给定一个区间，最值点对应的函数值只能有一个，达到最值的自变量点可能有多个；而该区间内的极值点可以有多个，这些极值点对应的函数值也可能大小不一。容易知道，最值是一个特殊的极值。也很显然，如果要找某个区间的最大值点，只需要把该区间里的所有极值点拿出来，挑对应函数值最大的那些就是了。

图C-3 信号的最值点与极值点

定理C-1（极值定理）对于函数取值为实数的函数f（t），如果在区间（a，b）上可微（或可导），那么区间里一点t₀∈（a，b）是一个极值的充分必要条件是(www.daowen.com)

f＇（t₀）=0（C-4）

我们继续讨论两个信号的线性相似度问题。这里我们先假设f₁（t）、f₂（t）都是函数值取值为实数的函数，C也是实数。那么，把式（C-3）展开成变量C的函数，即

要使g（C）最小，即为找函数g（C）一个最值点。而g（C）是在任何有限点都可微（可导）的，所以先找出所有有限极值点比较即可。根据极点定理，对g（C）关于C求导数得到g＇（C），

令g＇（C）=0，可得

观察到只有一个有限极值点，它可能是最值点。但是，注意还有正负无穷大没有考虑进来。当C趋于正无穷大或负无穷大时，有可能比求出来的有限极点的对应的函数值小吗？再结合一些基础知识可以这样判断，式（C-3）是关于变量C的开口向上的二次函数（高中数学二次函数应该大家都被折磨得比较多吧），只有一个最小值点，从而该极小值点一定是该最小值点。

根据上面的讨论，知道信号

是f₁（t）关于f₂（t）的最佳线性近似。假设把f₂（t）固定，看其他不同信号与它的线性相似性，我们会发现差别在分子的乘积积分，既然如此，我们干脆把它定义成一种运算好了，即所谓的相关运算或相关函数。

定义C-3（相关函数）如下定义的函数：

称为f₁（t）和f₂（t）的相关函数。

也许有人发现，式（C-9）定义的相关函数和上面推导过程中的形式上有所变化，用了共轭号。没错，我们这里做了推广，把相关函数推广到了函数值可以取值为复数的函数上。特别地，当信号f₁（t）=f₂（t）时，相关函数称为信号f₁（t）的自相关函数。另外，上面的定义适合于能量信号，若f₁（t），f₂（t）为功率信号，在时间上做个平均即可，不细讲了。

另一方面，由Cauchy-Schwarz不等式知

当且仅当f₁（t）=kf₂（t-子）时取得等号，即完全满足线性关系时取得等号。特别地，若f₂（t）=f₁（t），什么时候f₁（t-子）一定能保证和f₁（t）完全满足线性关系呢？显然 子=0时一定能保证，

从而

即自相关函数的模在零点取得最大值。

4.卷积运算

先看一个组合恒等式，相信大家略有印象，

推导很简单，一共a+b个不同的球，计算从中取出n个球的不同选取方法，显然一共有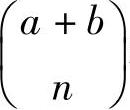种不同方法；另一种操作方法，先把球分成两堆，一堆a个，另一堆b个，要选总共n个出来，可以先在a个的那一堆里挑i个，再从b个的那一堆里挑n-i个出来一共凑成n个，对所有可能的i求和，就得到所有的挑选方法，即等式左边。

再看一个更复杂的恒等式。

定理C-2（Gould-Vandermonde卷积）对于任意的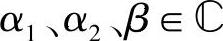，n>0，成立

对α₁、α₂、β、n取具体值，可以得到很多特殊形式的等式，此处不一一列举。有兴趣的读者，可以想想还能找到和式（C-12）一样简单的解释吗？

上面这种形式的等式在组合数学里有很多，被统称为卷积。把上面的和式推广成积分，组合表达式推广到一般函数表达式，则得到函数之间的卷积运算。

定义C-4（卷积运算）信号f（t）和g（t）的卷积信号记为，定义如下：

卷积运算满足对称性