可以将多个随机变量联合起来整体考虑，相应的分布函数称为联合分布函数。例如，两个随机变量X和Y的联合分布函数P（x，y）=P（X=x，Y=y）表示所有可能的事件对[X=x，Y=y]中，每一对出现的概率，满足

同样，可以定义多个随机变量的联合概率密度函数。例如，两个随机变量X和Y的联合概率密度函数f（x，y）=f（X=x，Y=y）满足

∫+-∫+-f（x，y）dxdy=1

且有

注意，多个随机变量独立考虑各自的分布函数或概率密度函数，与联合考虑分布函数等一般都是有差别的。为了区别，有些资料上会加个下标以示区别。比如关于随机变量X的分布函数写成P_X（X=x），引入边际分布的概念等。本书在不引起混淆的情况下，取消这个下标，读者朋友注意上下文区别就好了。

定义B-8（条件概率）随机变量Y=y已经确定时，随机变量X=x的概率为条件概率

条件概率其实是由联合概率P（X，Y）引导出来的一个概率。首先，当Y=y确定，对于不同X=x出现的可能性的相对关系本来就可以由联合概率P（X=x，Y=y）来刻画。但一般我们讨论概率时，都要求所有参加讨论的事件的概率之和为1。所以，我们把上面讨论的事件的概率归一化就可以得到条件概率。

性质B-2

另外，可以看到这里的条件概率形式上和前面讲事件的条件概率很相似，但我们已经说明是有区别的，提醒注意一下。

定义B-9（独立随机变量）如果两个随机变量的联合分布满足

P（X=x，Y=y）=P（X=x）P（Y=y）（B-11）

或者，联合概率密度满足

f（X=x，Y=y）=f（X=x）f（Y=y）（B-12）

那么X和Y称为两个独立的随机变量。

这个定义只是独立随机变量的量化定义，实际意义是说，由X确定的任何事件发生的概率不以已知的任何关于Y的信息而发生改变，反之亦然。(www.daowen.com)

那么，如果两个随机变量X和Y是定义在同一个概率空间上得到的随机变量，它们之间有可能独立吗？和上一节讲两事件之间的独立性时一样，没这个可能。

例B-4在例B-1中定义的概率空间[Ω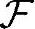，，P]上，定义随机变量X和Y。其中，X的定义同例B-2，定义随机变量Y如下：

Y（A）=1，Y（B）=2，Y（C）=2

则随机变量Y的分布函数为

考虑X=2，Y=2同时出现的概率P（X=2，Y=2）。首先，X=2表示B出现，Y=2表示或者B出现，或者C出现。那么，要想X=2，Y=2同时出现，只能是B出现。从而X=2，Y=2同时出现的概率等于B出现的概率，即

说到“同一个概率空间”，有必要多解释说明一下其意思。假设同时掷两个完全一样的股子，或同一个股子掷两次（两次实验），每次投掷里各点数出现的概率都是一样的。如果要写成概率空间的形式，两次投掷各自写出来的概率空间是相同的。但上面提到的“同一个概率空间”，不仅指写出来的概率空间数量形式相同，而且要求是刻画同一次实验的。这里描述的多次实验情形称为独立同分布，而不是同一概率空间的概念。显然，两个随机变量若是分别定义在两个独立同分布实验对应的概率空间上，那么它们肯定是独立的。

最后再做一点推广，我们把随机变量可以推广到随机向量，那么联合概率其实就是描述了随机向量的概率分布。特别地，我们把具有两个随机变量的随机向量可以定义成复随机变量来考虑，即两个随机变量X和Y可以看成一个复随机变量X+jY。该复随机变量的概率分布就是联合概率分布P（X，Y）。从而进一步，复随机变量可以推广成复随机向量。

定义B-10（循环对称复随机变量）对于复随机变量z=x+jy，其中x，y为实数随机变量。如果对于任意θ，复随机变量e^jθz和复随机变量z的概率分布完全一样，那么称复随机变量z具有循环对称性。

举个例子来说，如果复随机变量z=x+jy是均值为E[z]=0的复数高斯变量，那么复随机变量z就是循环对称复随机变量。因为

z＇=（x+jy）e^jθ=（xcosθ-ysinθ）+j（xsinθ+ycosθ）（B-13）

根据高斯变量的性质，可以检验z＇的实部和虚部仍然是高斯变量，且功率不变，并且实部和虚部独立，所以z和z＇概率分布相同。

定义B-11（循环对称随机向量）对于随机向量x=[x₁，…，x_m]，其中x_i为复数随机变量。如果对于任意θ，随机向量e^jθx和随机向量x的概率分布完全一样，那么称随机向量x具有循环对称性。对于协方差为E[x^Hx]=K_x的循环对称高斯随机向量，被记做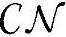（0，K_x）。

举个例子来说，如果每个随机变量x_i=x_iI+jx_iQ是均值为E[x_i]=0的复数高斯变量，且相互独立，那么随机向量x就是循环对称复随机变量。