定义B-3（分布函数）随机变量X上的函数

P（x）=P（X=x）=P（{ω|X（ω）=x}）（B-3）

称为X的分布函数，有∑_xP（x）=1。

例B-3 以例B-2定义的随机变量X为例，该随机变量可以取值1，2，3。概率分别为

上面的分布函数定义，适合在发生概率不为0的X仅为有限个的情况下使用。但是，当发生概率不为0的X有无穷多个时，每个特定取值的概率会趋于无穷小，不然所有概率之和不可能还等于1。此时，引入累积分布函数（Cumulative Distribution Function，CDF）和概率密度函数（Probability Density Function，PDF）更方便些。

定义B-4（累积分布函数）随机变量X上的函数

C（x）=P（X≤x）（B-4）

称为X的累积分布函数。

图B-1 随机变量X的累积分布函数(www.daowen.com)

利用累积分布函数，我们可以方便地查任何取值区间的随机变量发生的概率。例如，区间X∈[a，b]的概率为C（b）-C（a）。但是，当我们想分辨的区间粒度越来越小时，即[a，b]越来越窄时，问题又来了，因为我们发现C（b）-C（a）又会趋于无穷小。比如，对于累积分布函数来说，某个点X=x₀的概率为

X=x₁附近小区间的概率为无穷小，X=x₂附近小区间的概率为无穷小，也不方便。因为不管怎么样，它们总有差别嘛，总还是有大小关系嘛！那这个大小关系怎么体现出来？一种方法就是看各自的平均变化速度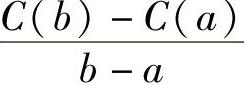。当b-a→0时，即为概率密度函数。

定义B-5（概率密度函数）随机变量X上的函数

称为X的概率密度函数，此时有

图B-2 随机变量X的概率密度函数

可以发现概率密度函数是累积分布函数的导数。对于概率密度函数来说，某个点X=x₀的概率为

另外，上面三种刻画随机变量出现概率的函数P（x）、C（x）、f（x）都是等价的，仅是使用方便程度上有差别。实际使用过程中，哪个好获得，用哪个吧。