定义B-2（随机变量）在概率空间[Ω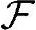，，P]中的样本空间上定义一个到实数域R上的函数X，要求取值相同的样本点组成的集合{ω|X（ω）=x}∈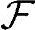，ω∈Ω，x∈R，则X为一个随机变量。

上面的定义中，对函数X的唯一一个限制是取值相同的样本点组成的集合{ω|X（ω）=x}∈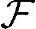，ω∈Ω，x∈R，之所以有这个限制，是因为我们还要描述随机变量的概率，而概率只定义在事件上；若某个随机变量取值对应的样本点集合不是概率空间的一个事件，那如何确定该随机变量取值的概率呢？

例B-2 概率空间[Ω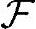，，P]，其中集合Ω={A，B，C}，集合

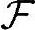={∅，{A}，{B}，{C}，{A，B}，{B，C}，{A，C}，{A，B，C}}

集合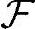上函数P为(www.daowen.com)

在样本点集合Ω上定义一个到实数域的函数X，

X（A）=1，X（B）=2，X（C）=3

则X为一个随机变量。

看起来，随机变量的引入是为了简化概率空间的表述，以免用集合这些东西来描述。比如，集合中的样本本来可以是任何形式的，函数、向量、矩阵、天气、猫猫狗狗，但是现在都统一表示成实数域R上的数了。事实上，应该是先有变量的想法，概率空间只是一个抽象的公理化概括。另一方面，虽然这里的随机变量的定义要先以一个存在的概率空间为基础，这只是为了给一个严格的理论支撑，主要是想说任何一个随机变量一定可以看成由至少一个概率空间产生，但这个概率空间在实际应用中不一定需要明确确定出来。在实际应用和讨论中，经常你是不能明确地看到正在讨论的随机变量是基于哪个概率空间定义出来的；而是，直接由其他特征来刻画了，比如接下来要讲的分布函数，概率密度函数等等；不管怎么样，接下来事件的概率都将被换成随机变量的语言了。