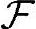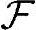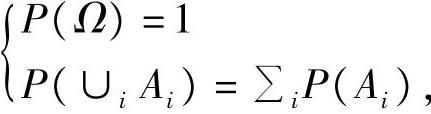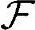定义B-1（概率空间）有一个集合Ω，为集合Ω的一些子集构成的集合，其中至少包括空集∅和全集Ω，P为定义在上的函数满足{_当A_i∈，且两两没有交集时

则三元组[Ω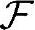，，P]构成一个概率空间，其中Ω中的元素称为样本点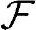，中的元素称为事件，P描述了每个事件在所有可能事件中发生的概率。

例B-1集合Ω={A，B，C}，集合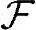={∅，{A}，{B}，{C}，{A，B}，{B，C}，{A，C}，{A，B，C}}，集合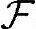上函数P为

则[Ω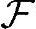，，P]为一个概率空间。

当然，上面的定义还不是最完整、最严格的，但从应用层面来说，这样足够了。

记P（X∪Y）表示X或者Y发生的概率，P（X∩Y）表示X和Y同时发生的概率，P（Y|X）表

示X已经发生了，Y能发生的概率，也称为条件概率。

性质B-1（基本命题）

上面第一条基本命题，其实就是由概率空间[Ω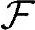，，P]诱导了（或称为隐含了）另一个概率空间[Ω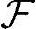＇，＇，P＇]。该新概率空间里样本点集合为Ω＇=Ω∩X，事件空间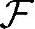＇为原事件空间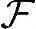里每个事件（即子集）与X的交集确定的事件组成的，概率P＇就是根据第一条基本命题由P推导如下得到的：假设该事件空间里任一事件Y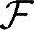＇∈＇，若有某个事件Y∈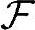使得Y＇=Y∩X，那么

只不过，现在我们都把事件Y＇写成Y|X的形式而已。所以严格来说，应该稍微区分一下，比如把P（Y|X）写成P＇（Y|X）。但在不产生混淆的情况下，我们还是不去特别区分。(www.daowen.com)

还有个小问题可能值得说明一下：这里的条件概率和稍后我们讲随机变量时的条件概率不完全是一回事。可能大家比较熟悉的是，如果两个事件独立，那么条件概率P（Y|X）=P（Y）。在这里这个条件概率没有这样的性质，因为这里的两个事件X，Y是属于同一个概率空间的两个事件，它们永远不可能有相互独立一说。即使X和Y没有交集，也不表示X和Y独立。因为此时，如果X发生了，Y发生的可能性就为0。例如，在例B-1中，有

有点抽象，大家好好理解一下。

第二条基本命题，基本上来说，可以认为概率函数P为事件空间上的一个线性函数。

因为

X∪Y=X+Y-X∩Y

从而

P（X∪Y）=P（X）+P（Y）-P（X∩Y）

可以看到，通过上面两条基本命题，把几种事件之间的运算对应的概率联系起来了。还有，上面两条其实也可以归结为概率空间的定义的一部分；在完整的概率空间定义中，事件空间里事件之间的相互关系，以及事件对应的概率之间的关系还有很多条款限制。这里就不多考虑了，如果实在有必要，到时再考虑进来。