线性空间上的正交变换及其矩阵表示

给定一个线性空间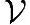和其上一组基{v₁，…，v_N}，f为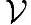上一个线性变换。那么，对于任意x∈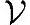，x=∑k_iv_i，在f的作用下得到的f（x）在基{v₁，…，v_N}下的坐标是多少呢？下面我们来解决这个问题。

首先，前面我们已经讲过如何求一个向量在一组基下的坐标了，我们只需要按部就班的应用即可。我们还假设线性空间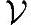里元素间定义了某个内积<，>，令

再假设，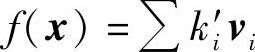

则

K＇=A^-1Y

看起来，Y可以进一步展开。那我们就把Y展开看看有什么发现：

从而f（x）的坐标进一步可以写成

K＇=A^-1BK

注意到，A^-1和B都和x具体为哪个向量无关，从而它们对于任何向量x建立了线性变换前后在同一组基下的坐标之间的关系。换句话说，这个时候线性变换f最开始定义的样子已经不重要了，不管你怎么定义，它总是可以借助于一个内积、一组基和一个对应矩阵A^-1B来刻画。可以看到，矩阵这一形式是十分有用的。

定义A-14（正交变换）在线性空间上的线性变换f，若对其上定义的内积<，>满足：对任意的x和y，

<x，y>=<f（x），f（y）>（A-25）

那么，称f为正交变换。

假设{v₁，v₂，…，v_N}是线性空间上一组标准正交基，且(https://www.daowen.com)

x=∑x_iv_i，y=∑y_iv_i

则，

<x，y>=∑x_iy_i=[x₁，…，x_N][y₁，…，y_N]^T

而根据上面的讨论知，f（x）和f（y）在该组基下的坐标为

[f（x）]_i=A^-1B[x₁，…，x_N]^T，[f（y）]_i=A^-1B[y₁，…，y_N]^T（A-26）

注意，因为这里是标准正交基，从而A=I单位阵。进而

再根据f是正交变换的定义，知

<f（x），f（y）>=<x，y>

从而，必然有

B^TB=I

定义A-15（正交矩阵，酉阵）实数域上的矩阵B若满足B^TB=I，则称为正交矩阵；复数域上的矩阵B若满足B^HB=I则称为酉阵，其中B^H表示B的共轭转置。那么上面的讨论即是说，一个正交变换在给定一组正交基的情况下，其效果对应于一个正交矩阵；当然，如果在复数域上考虑，对应于一个酉阵。