定义A-12（一一映射）两个集合U和V，从集合U中的元素到集合V中的元素定义一个对应关系f，使得在这个关系下，U中的任何一个元素只唯一对应到V中的一个元素，并且V中的任何一个元素也能找到唯一一个U中的元素和它对应，则对应关系f称为U到V的一一映射。

显然，一一映射要求集合U和V包含相同个数的元素。

定义A-13（线性映射）两个集合U和V，从集合U中的元素到集合V中的元素定义一个对应关系f，满足

f（u₁+u₂）=f（u₁）+f（u₂）

f（ku）=kf（u）那么，称f为U到V的一个线性映射。既是一一映射，又是线性映射，称为一一线性映射。特别地，线性空间到自身的一一线性映射称为线性变换。

性质A-10（基变换）若{v₁，v₂，…}是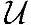上的一个线性无关组，f是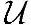到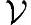上的一个一一线性映射，那么，{f（v₁），f（v₂），…}是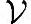上一个线性无关组。(www.daowen.com)

证明 考虑如下等式何时成立，

∑k_if（v_i）=f（∑k_iv_i）=0

因为f是一一线性映射，上面等式当且仅当∑k_iv_i=0时成立。而{v₁，v₂，…}是一个线性无关组，则∑k_iv_i=0当且仅当所有k_i=0成立。从而，根据无关向量组的定义知向量组{f（v₁），f（v₂），…}无关。

可以看到一一线性映射把一个空间的一组基变到另一个空间的一组基，从而只要知道线性映射在一组基上的效果就能完全确定该线性映射在所有向量上的效果。后续应用时，咱们再聊。