定义A-8（最佳近似）向量x和向量集合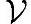，向量间数域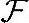上的内积为<，>，向量y∈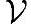被称为向量x在向量集合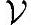上的最佳近似，如果满足

即，在所定义的内积<，>下，y与x距离最小。上面的最佳近似定义在任何集合上，但如果集合V是一个线性空间，那么又如何呢？

定义A-9（最佳线性近似）向量x∈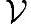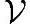，＇是线性空间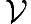的一个子空间，且其子空间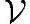＇的一组基为{v₁，v₂，…，v_m}，则向量x在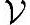＇里的最佳近似x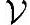＇∈＇被称为向量x关于向量组{v₁，v₂，…，v_m}的最佳线性近似。

之所以称为最佳线性近似，是因为x＇能表示成{v₁，v₂，…，v_m}的线性组合。

定理A-5（正交原理）内积空间V里的一个向量x在该内积空间的一个子空间V＇里的最佳近似为x＇，且其子空间V＇的一组基为{v₁，v₂，…，v_m}，则x-x＇和子空间V＇的所有基v_i分别正交，从而也和子空间V＇里所有向量正交。

证明 设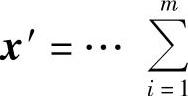C_iv_i，为x的最佳线性近似。考虑

其中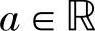.上面看成a的函数，根据极点的处理方法，求达到极值时a的取值，可得

又因为，上面式子是关于a的开口向上的二次函数，该唯一的极值点为达到最小值点。而我们上面的假设，已经知道x＇已经是最佳近似了，即已经达到最小值点了，所以必然a=0，从而有

R_eal{<x-x＇，v_j>}=0再考虑

其中.仍然看成a的函数，并且求最小值得

而我们上面的假设，已经知道x＇已经是最佳近似了，所以也有a=0，从而有

Imag{<x-x＇，v_j>}=0

综上所述，得

<x-x＇，v_j>=0

即x-x＇与子空间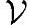＇的任意一个基向量正交。而线性子空间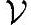＇里的任何一个向量y是基向量v_j的组合，不妨设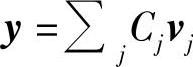，则显然

即x-x＇与子空间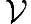＇中任何向量都正交。

性质A-7（计算最佳线性近似）设内积空间V里的一个子空间V＇，其子空间V＇的一组基为

{v₁，v₂，…，v_m}一个向量x在该内积空间的子空间V＇里的最佳近似为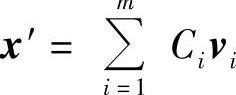。记

那么，(www.daowen.com)

C=A^-1Y（A-22）

特别地，当{v₁，v₂，…，v_m}是一组正交基时，

证明 由上面的正交原理得

当v_j中j遍历1，…，m得到m个方程，即

AC=Y

展开整理即得证。

大家注意到什么没有？看起来似乎像求坐标的方法？没错。假设N维线性空间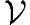的一组基为{v₁，…，v_N}，向量

x=C₁v₁+…+C_Nv_N

对于任何由该组基中部分基向量{v_k1，v_k2，…，v_km}组成的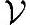的一个线性子空间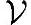＇，向量x在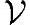＇中的最佳近似就是x＇=C_k1v_k1+C_k2v_k2+…+C_kmv_km。

知识扩展 上面讲正交原理时，为什么要要求是线性空间呢？假设集合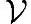不是线性空间会怎么样？还可能正交吗？答案是不可能。

证明 采用反证法。如果对任意的集合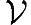，集合中与向量x距离最近的向量y有

<x-y，y>=0

那么，把y从集合V中拿掉。在剩下的集合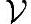-y里，找到与x距离最近的，假设为y＇。那么，也应该有

<x-y＇，y＇>=0

再把y＇从集合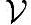-y里拿掉，一直继续找与x距离最近的。最后，我们得到如下结论：对于任意的集合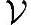中的任意一个向量y∈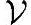，总是有

<x-y，y>=0

这有可能吗？应该没这个可能。

而如果说只有当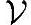是线性空间才成立，那么你会发现，把一个向量y从线性空间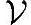中拿掉，剩下的集合就不是线性空间了，从而也就不会有上面那样荒谬的逻辑。