下面我们再介绍一些常用且重要的量化关系。

定理A-1（Cauchy-Schwarz不等式）对于定义在任意数域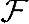上的内积，我们有

当且仅当y=kx，k∈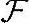时等号成立。

证明 如果y=0，不等式显然成立。如果y≠0，则<y，y>≠0，取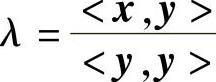。因为

<x-λy，x-λy>≥0

则有

整理可得。

这个不等式很重要，比如匹配滤波、某些最大似然算法设计等都是以它为基础的。

应用（匹配滤波） 假设有几个信号f_i（t）满足能量相等，即

∫f_i（t）f_i（t）*dt=∫f_j（t）f_j（t）*dt

并且它们两两之间没有线性关系。现在发射端随机发送其中一个，接收端怎么判断是其中哪一个呢？

所谓判断是指基于某种特别的特征来做出决定，尤其是一些极端特征，比如通过某种处理会得到0，或者达到最大值、最小值之类的。因此这个问题可以这样解决：

记收到的信号为f（t），把所有的可能信号f_i（t）拿来和收到的f（t）做内积

而我们又知道只有当f_i（t）=kf（t）时，才可能达到这个常数值。又因为，f_i（t）里面两两没有线性关系，也即只有自己跟自己才会有线性关系，必然只有f_i（t）=f（t）时，才能达到该常数值，从而能判断出发射端发射的是哪个信号。(www.daowen.com)

考虑：如果f_i（t）两两能量不同，又或者如果f_i（t）里面某些之间有线性关系会怎样？留做练习思考。

定理A-2（三角不等式）

当且仅当y=kx，k∈R^+时，取得等号。

证明 首先，

整理可得三角不等式。

下面考虑取等号的条件：注意到上面第一步“≤”要取得等号的前提是

Real{<x，y>}≥0，Imag{<x，y>}=0

第二步“≤”要取得等号的前提是y=kx，从而有

●虚部Imag{<x，kx>}=0，得k∈R。

●实部Real{<x，kx>}≥0，得k≥0。

故当且仅当y=kx，k∈R^+时，取得等号。

可以提一下的是，三角不等式最简单的体现形式就是大家小学就应该知道的三角形两边之和大于第三边啦。