在一个线性空间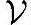上定义一个二元运算<，>，该二元运算的结果为数域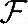上的数，这里先只考虑实数域R和复数域■，并且满足如下几条性质：

●<x，y>=<y，x>*；

●<kx，y>=k<x，y>，k∈；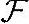

●<x+y，z>=<x，z>+<y，z>；

●<x，x>=<x，x>*≥0，当且仅当x=0（线性空间零元）时等号成立。

那么，该运算称为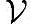上的一个内积。定义了内积的线性空间，也称为内积空间。注意，当数域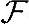是实数域时，共轭号没什么作用，可以省略。但为了保持一致性，一般情况我们都保留。

上面的几条性质是内积满足的最小完备集合，其他性质可以由上面的性质推导出来，例如：

性质A-2 x，y∈v，k∈F，则有

<x，ky>=k*<x，y>（A-7）

证明

<x，ky>=<ky，x>*=（k<y，x>）*

=k*<y，x>*=k*<x，y>

下面列举一些内积运算的例子，读者朋友可自行验证一下它们是否都满足上面的内积定义。(www.daowen.com)

【例A-1】 在一般有限维数组组成的集合上定义内积如下：

【例A-2】 在一元函数组成的集合上定义内积如下：

<f（t），g（t）>=∫f（t）g（t）*dt（A-9）

【例A-3】 在随机变量（注意目前为止都认为随机变量取值为实数）组成的集合上定义内积如下：

<X，Y>=E[XY]（A-10）

或者

<X，Y>=E[（X-E[X]）（Y-E[Y]）]（A-11）

本书后续讨论中，如果讨论的对象为这些常规集合中的元素，那么若无特殊说明，用到的内积都是这些常规内积。

可以看到，依托在集合中引入内积定义，每个集合中的元素，不管是函数、随机变量、矩阵或其他多么稀奇古怪的形式，它们最后两两都对应到一个数域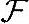上的数，从而相互之间在某种程度上有了量化关系。

特别地，任何集合中的元素x，其与自己的内积<x，x>都对应到实数域R上的一个数，从而可以看到内积运算<x，x>在集合V上定义了一个范数（norm），我们也把x的这类范数（或者称为模）记为

同时，有了内积，还可以定义两个对象x，y之间的距离D（x，y）