定义A-1（线性无关）线性空间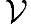上一组向量{v₁，v₂，…}，若其所有线性组合∑k_iv_i中，当且仅当所有k_i=0时才得到0，那么该组向量被称为无关向量组。

性质A-1 线性空间中，如果一个非0向量v能由向量组{v₁，v₂，…}唯一线性表示出来，那么向量组{v₁，v₂，…}必然是一个无关向量组；反之，如果一个非0向量v能由向量组{v₁，v₂，…}线性表示出来，且该向量组是一个无关向量组，那么表示方法必然唯一。

证明 只证明前半部分，后半部分类似。

假设唯一表示为

如果向量组是相关的，那么必然能找到一组不完全为0的系数p_i，使得

从而有

因为p_i不全为0，该表示方法必然构成v的另一种不同的线性表示方法，矛盾。(www.daowen.com)

可以拿线性空间定义来逐条检验得到，任何一个无关向量组的所有线性组合生成的集合也是线性空间。还可以简单证明，一个无关向量组里一部分向量组成的子组也是无关的。

定义A-2（基与坐标）线性空间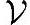上一组向量{v₁，v₂，…}，若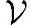中任意向量都可以表示成它们的线性组合，称该向量组为该线性空间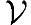的一组基。可以证明，任意向量v=∑k_iv_i中，系数k_i是唯一的，该组系数被称为向量v在基{v₁，v₂，…}下的坐标。线性空间的一组基中所包含的向量个数称为该线性空间的维数；维数可以有限，可以无限。

记线性无关组{v₁，v₂，…}的所有线性组合生成的线性空间为<{v₁，v₂，…}>。显然，向量组{v₁，v₂，…}就是线性空间<{v₁，v₂，…}>的一组基。

定义A-3（线性子空间）线性空间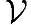的一个子集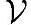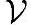＇■，如果在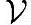上相同运算“+”和运算“·”下也构成线性空间，那么线性空间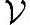＇称为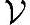的线性子空间。相对地，线性空间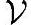可以称为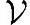＇的扩展空间。

当然无关向量组的任何一个无关子组的所有线性组合生成的集合也是线性空间，并且该无关子组是该线性空间的一组基，该线性空间是原来无关（母）组生成的更大线性空间的一个线性子空间。

为什么要研究线性空间的基呢？首先，当然是因为应用分解的思想，引出了把一个向量分解成其他向量的线性组合；其次，是为了给定一个后续可以比较研究同一线性空间里不同向量之间关系和运算等的统一参考标准。例如，假设所有人构成一个线性空间（虽然这里不能清楚定义两个人“相加”还属于这个线性空间是什么意思）。这里有路人甲的（身高、体重、三围、…）外在生理特征，而仅有路人乙的（性格、兴趣爱好、偶像、…）精神层面特征，现在让你说说两个人的差别，你从哪里入手说起呢？不知如何下手吧，为什么？标准不统一啊！话说有哪些统一标准呢？指纹算吧，DNA也算一个吧。这个世界上，除了同卵双胞胎可能一样外，每个人的DNA都是不一样的。学过点生物的都知道，DNA就是两条链的双螺旋结构，每条链仅由四个不同的碱基（A、C、G、T）排列而成，也就是说每条链就是一个由四个不同元素组成的序列，那就是一个向量嘛！所以，路人甲乙丙丁分别就是一个向量，所有人说成线性空间好像也可以，只不过该线性空间中有些向量还没有实体呈现出来（还没有来过这个世上）。