在一个集合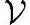上定义一个二元运算，记为“+”，与数域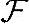联合定义一个运算，记为“·”，且满足如下性质：

●交换律：v₁+v₂=v₂+v₁；

●结合律：（v₁+v₂）+v₃=v₁+（v₂+v₃）；

●零元素：在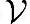中有唯一一元素，记为“0”，对于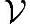中任一元素v有v+0=v；

●负元素：对于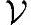中每一个元素v₁，有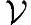中的唯一元素v₂，使得v₁+v₂=0；

●k（lv₁）=（kl）v₁，k，l∈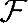；(www.daowen.com)

●（k+l）v₁=kv₁+lv₁；

●k（v₁+v₂）=kv₁+kv₂。

则，集合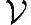在加运算和乘运算下为一个数域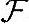上的线性空间（Linear Space），其中元素称为向量。

现在假设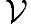已经是线性空间了，看看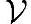里的元素结构怎样。首先任意取一个v₁≠0，把所有kv₁拿掉，注意0=0v₁被拿出来了，剩下的集合里再不会有0；接着在剩下的集合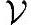-{kv₁}里任意取一个v₂，把所有k₁v₁+k₂v₂的元素从中拿出来，一直这样继续下去，最后所有元素都被拿出来了，从而也得到一系列向量[v₁，v₂，…]。可以看到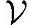里任何向量都是以k₁v₁+k₂v₂+…的形式被拿出来的，也就是说都可以表示成k₁v₁+k₂v₂+…的形式，并且只有当k_i全等于0时，∑k_iv_i=0，因为在上面的操作中，第一次就把0拿出来了（相当于k₁=0，k_i≥2=0时），而后面的操作相当于遍历了所有k_i不全为0的情况都没得到0。所以，可以看到任何一个线性空间总是存在这样一系列向量，使得任意向量都可以表示成它们的线性组合。注意，这里体现了分解与组合的基本思想，可见其无处不在啊。