1.一般系统的信道容量

讨论一般MIMO系统的信道容量，仍然可以根据推广的互信息来计算。假设一共有t个发射天线，有r根接收天线，信道矩阵H_r×t为接收端所知，各天线发射数据为x=[x₁，…，x_t]，其中各天线信号功率为E{x_i²}=P_i，信号总功率为

E{x²}=P并记各天线发射数据的相关矩阵

K_x=[x₁，…，x_t]^H[x₁，…，x_t]那么，显然相关矩阵K_x的迹有Tr{K_x}=P。则，接收到的信号为

y=Hx^T+w该MIMO系统信道容量表示成互信息为

首先对于给定信道矩阵H，条件互信息

其中，当且仅当发射的数据x是循环对称（Cyclic Symmetric）高斯随机向量时取得等号。从而此时的信道容量满足

其中，当且仅当发射的数据x是循环对称随机向量时取得等号。当遍历所有功率分配情形时，也即遍历满足Tr{K_x}=P的所有循环对称随机向量，找到最大值就可得到该系统的信道容量为

固定信道作为一种特殊情形，假设信道固定为H，该信道容量为

和SISO系统类似，MIMO信道也可以讨论随机慢衰落信道的溢出容量和溢出概率等，这里不做深入讨论了。(www.daowen.com)

2.一般正交系统的信道容量

对于有t根发射天线，r根接收天线的MIMO系统，基于该MIMO系统的正交系统如下：给定一个正交矩阵Q_t×t，信号携带在矩阵Q的列向量上发射出去，携带在各列向量上信号相互独立（没有联合编码）。该通信系统模型为

y=HQx+w

其中，x=[x₁，…，x_t]^T，且E{x_i²}=P_i。当某个P_i=0时，表示实际上没发信号x_i。又因为假设x_i相互独立，那么相关矩阵K_x=diag{P₁，…，P_t}为对角阵。根据上一节讲的信道容量可知，该正交系统的信道容量为

当且仅当每个x_i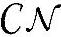～（0，P_i）即可达到该信道容量。特别地，若是所有x_i等功率分配，即K_x=diag，那么信道容量为

可以看到，对于平均分配功率，信道容量和正交系统Q无关，即任何正交系统的信道容量相等，只取决于信道本身。再特别地，当Q=V时，且V随H变化而相应变化，信道容量为

当且仅当每个x_i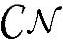～（0，P_i）即可达到该信道容量，和矩阵奇异向量系统的结果一致。并且上面式子里若是等功率分配P_i=P/t，显然也能说明任何正交系统的信道容量相等，因为连奇异向量系统也是一样的信道容量。最后，进一步，若发射端知道信道，可以采用注水定理进行功率分配达到最优。

上面讲了一些基本的发射接收算法思想，更多具体发射接收算法，比如贝尔实验室提出的BLAST系列算法等，本书就不具体详细讨论了，请读者朋友自行查阅资料。