假设信道是不变的，即信道矩阵H_r×t是固定的，且为发射端所知，其秩为L。发射端采用信道奇异向量系统进行数据发射且发射了k≤L个数据流，各个数据流独立编码，那么该系统的信道容量是多少？我们知道奇异向量系统在接收端来看就等价于k个并行的SISO信道（MRC合并前为k个并行的SIMO信道），而各个数据流独立编码，那么信道容量为k个并行信道容量之和。

假设发射端总功率为P，第i个数据流经历的等价SISO信道为λ_ix_i+N_i，其中λ_i为第i个奇异值，第i路分得的信号功率为P_i，∑_iP_i=P，N_i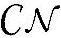～（0，σ²）。那么，第i个信道的信道容量为

从而该MIMO系统信道容量为

达到该容量的编码方式为各数据流像在AWGN下各自达到信道容量一样即可。

上面的讨论是把发射的数据流个数和每个流的功率分配固定下来讨论信道容量，如果保持数据流个数不变，放开每个数据流的功率限制，即功率在保持总功率的情况下可以灵活分配。那么，当遍历所有功率分配可能性时，信道容量最大的情况是什么呢？

这个优化问题已经不是新问题了，答案就是注水定理：λ²_i越大，对应的数据流分配的功率越多，反之越少，甚至没有。最佳分配功率为

其中，λ的取值要满足

注意到，根据注水定理分配功率，有可能某个数据流的分配功率为0，那么实际上这个对应的数据流相当于不传输数据，也就是说，此时真正传输的数据流个数不是k个，从而该优化问题的前提条件准确说应该写成“当最大数据流个数不超过k个时的最大容量问题”。从另一个角度来说，其实k没必要限制到k≤L，而是可以限制到k≤min{t，r}。因为对于那些奇异值为0的数据流，按注水定理是不会给它们分配功率的。也就是说，即使把k的限制放宽，放宽出来的对应于奇异值为0的数据流是不会用来传输数据的，实质上不会产生影响。

当允许的最大数据流个数k增大，其遍历功率分配情况的信道容量一定不会减小，因为最大数据流个数小的优化问题是最大数据流个数大的一个功率分配情况的子集，即多出来的那些功率总是为0。那我们接下来就以信道允许的最大数据流个数L来继续讨论信道容量，当然最优功率分配还是满足注水定理，就不赘述了。

本章前面开始讲空分复用原理的时候，各数据流地位是平等的。现在我们看到，在有噪声的实际信道中，各数据流的地位慢慢变得不平等了，比如这里的最优功率分配就使得各数据流信号功率不一样。

特别地，当各个流功率分配相等时，即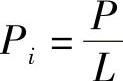，信道容量

其中，det为行列式运算符。那么，我们看到平均分配功率时，信道容量只取决于信道相关矩阵HH^H，即取决于各收发天线间信道的相关性。当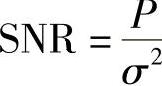较高时，有(www.daowen.com)

从而

注意到这个容量后半部分是由信道本身确定的，是不能被人为改变的，前面部分和功率使用情况相关。我们知道如果是SNR较高的SISO系统，其最大信道容量为log（1+SNR）≈log SNR。也即是说，当SNR高时，式（16-25）所示的多天线系统的信道容量相对于相同SNR的单天线系统来说，呈L倍线性增长。前面，我们在讨论香农容量公式的时候也讲过，当SNR很高时，信道容量其实对信号功率是不敏感的；即功率上的一点差别，并不会带来多大的信道容量差别。所以，当SNR很高时，虽然按照注水定理得到的最佳功率分配仍然一般各不相同，但是平均功率分配和最佳功率分配得到的信道容量差别不大。因此，在SNR很高时，平均功率分配的信道容量几乎趋近于最佳容量。

再者，平均功率分配时的信道容量

其中，不等式≤利用了log（1+x）凸函数性质詹森（Jensen）不等式

7当且仅当x_i相等时取得等号，即式（16-26）所示的容量公式中当且仅当所有λ_i相等时，取得等号。也就是说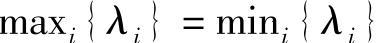，i{λ_i}时，信道容量达到最大值。事实上，理论分析可以证明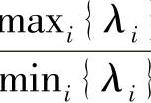，越趋近于1，信道容量越大。通常也把比值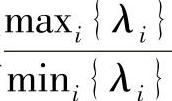定义为信道矩阵H的条件数（Condition Number）。

另一方面，从信道矩阵的SVD可以知道

那么，在高SNR区域，信道容量C满足

也就是说，在高SNR且等功率分配时，所有信道总增益∑h_ij²相同的信道，信道容量上限差不多，就看哪个信道的条件数低了。条件数越低，就越接近这个信道容量上限。

而当SNR较低时，任何功率分配

当把所有功率分配给奇异值最大的数据流时，信道容量最大。注意，这里并不是说注水定理的最后结果一定是所有功率都分配给奇异值最大的数据流，其他流功率为0。这要求首先要在第一步的近似“≈”非常准确时，这两个才完全一致。通常情况下，各个数据流理论上可能还是分别有点功率的，并不会真正为0。