从信道矩阵的SVD分解可以看出，信道矩阵H的秩等于SVD分解中对角矩阵中的对角元素λ_i中非0元素个数。

前面我们已经提到每个数据流在映射到天线时是乘以一个向量，也就是说发射端发射了一个t维向量，而经过信道以后，接收端接收到了一个r维向量。因为U、V是酉阵，所以它们各自的行向量或者列向量构成其对应维数的向量空间的基，那么其他任何一个同维数（同一空间）的向量都可以由它们线性表示出来。

例如，发射端发射的x_jW_j可以表示成

若W_j=1，那么有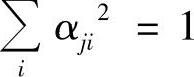，则经过信道后，接收端接收到

自然地，若发射端发射了数据流为

接收端收到的信号为

理想情况下，只要x_j对应的向量组[（α_j1λ₁）U₁+（α_j2λ₂）U₂+…]是无关向量组，就可以还原x_j了。注意到，若信道矩阵的秩为L≤min{t，r}，即当i>L时λ_i=0，那么向量组[（α_j1λ₁）U₁+（α_j2λ₂）U₂+…]实际形如[（α_j1λ₁）U₁+（α_j2λ₂）U₂+…+（α_jLλ_L）U_L]。也就是说，所有x_j对应的向量是向量组{U₁，…，U_L}生成的空间里的向量，显然这个空间里最多能找到L个无关向量。因此，该信道最多能分离L个数据流x_j。

如果发射端把数据x₁携带在向量V_j上，且j>min{r，t}或者不幸对应的λ_j=0，j≤min{r，t}，此时会有接收信号

H（x₁V_j）=0

这样的话，接收端能得知x₁是多少吗？如果发射端把数据L=[x₁，x₂，…，x_L]，用预编码矩阵W=[V_j，V_j+1，…，Vj+L-1]进行预编码后发射，其中V_j，…，V_j+L-1对应的λ_j，…，λ_j+L-1都等于0，则会有

HWL=0理论上，接收端什么都解不出来。可以看到，即使H的秩为L，预编码矩阵W也是列满秩的，有时也不能支持L层数据流的传输，需要选择合适的预编码W才行。(www.daowen.com)

如何确定预编码W呢？MIMO系统里，一种较简单的预编码方法就是把要传输的数据流携带在相互正交的向量上发射出去，我们把这样的发射系统称为正交系统。这样做的好处是，接收端处理比较简单，因为信道（矩阵）作为线性映射会把发射端正交向量变成接收端正交向量，从而从接收端来看数据流也是被携带在相互正交的向量上。

我们先看例子：假设信道的秩为L，把k≤L层数据流[x₁，…，x_k]^T分别携带在信道矩阵H=U∑V^H中V的列向量V₁，…，V_k上，则发射出去的是

x₁V₁+…+x_kV_k

我们把用信道（右）奇异向量（如V_i）携带数据的系统称为奇异向量系统。发射端信号经过信道，接收端收到的信号是

λ₁x₁^U1+…+λ_kx_kU_k+N其中，N为噪声，那么，解调x_i很简单，不用管其他x_j，就像SIMO系统里发射了x_i，到接收天线经过的信道衰落为λ_iU_i一样，在没有额外干扰时用MRC就是不错的接收方法。以解x₁为例，应用MRC，有

注意到，其他x_i（i≠1）的项都被变成0了，是不是很简单？就像并行独立的k个SISO信道一样，x_i相互之间没什么牵连。从这里，我们还可以清晰看到，如果信道矩阵有L个非0奇异值，那么确实可以并行传输L个数据；并且如果发射端知道信道矩阵H，我们也看到了采用怎么样的预编码实际能完成L流数据传输，比如采用L个非0奇异值对应的（右）奇异向量。

对于一般的正交系统Q，发射端发射Qx，接收端收到HQx，应用MRC合并得

x＇=（HQ）HHQx=[λ₁＇x₁，…，λ_k＇x_k]^T

也就是说，一般正交系统Q也是平行信道，但不一定有λ_i＇=λ_i。甚至如上面讨论，有可能某些λ_i＇=0，那么x_i就白传了，解不出来。

实际系统中，发射端可能并不知道信道H是什么样子，也就不知道V是什么样子。没关系，随便确定一个正交系统，即随便给定k个相互正交向量就好，但是有可能不巧的是，你给定的正交向量中，有些携带信号经过信道后可能会被变成0，那这些向量上携带的数据就遭殃了。这个问题，可能需要接收端反馈或其他手段来解决，这些内容以后再讲。