1.SVD分解

矩阵奇异值分解（Singular Value Decomposition，SVD）是说，任何一个矩阵H_r×t=[h_ij]，h_ij∈■都可以分解成如下形式：

H=U∑V^H

其中，

U，V都是酉阵（复数域上的标准正交方阵）。矩阵∑是r×t的对角阵，记为

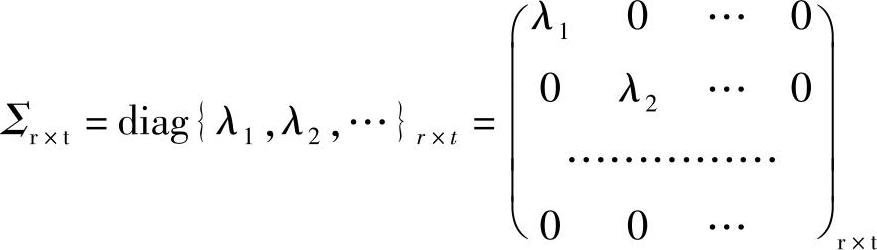
该分解形式中，对角阵∑中若要求其min（t，r）个对角元素λ_i按从大到小排列λ₁≥λ₂≥…≥λ_min（r，t）≥0，那么∑是唯一的，但U、V不一定唯一。其中，λ_i称为矩阵H的奇异值，矩阵U中的列向量U_i称为矩阵的左奇异向量，矩阵V中的列向量V_i称为矩阵的右奇异向量。假设一个4发4收的信道H₄×4，信道矩阵中每个元素h_ij是独立的瑞利衰落时，其奇异值的分布如图16-5所示，其中λ₁表示最大奇异值的概率密度分布情况，λ₄表示最小奇异值的概率密度分布情况。

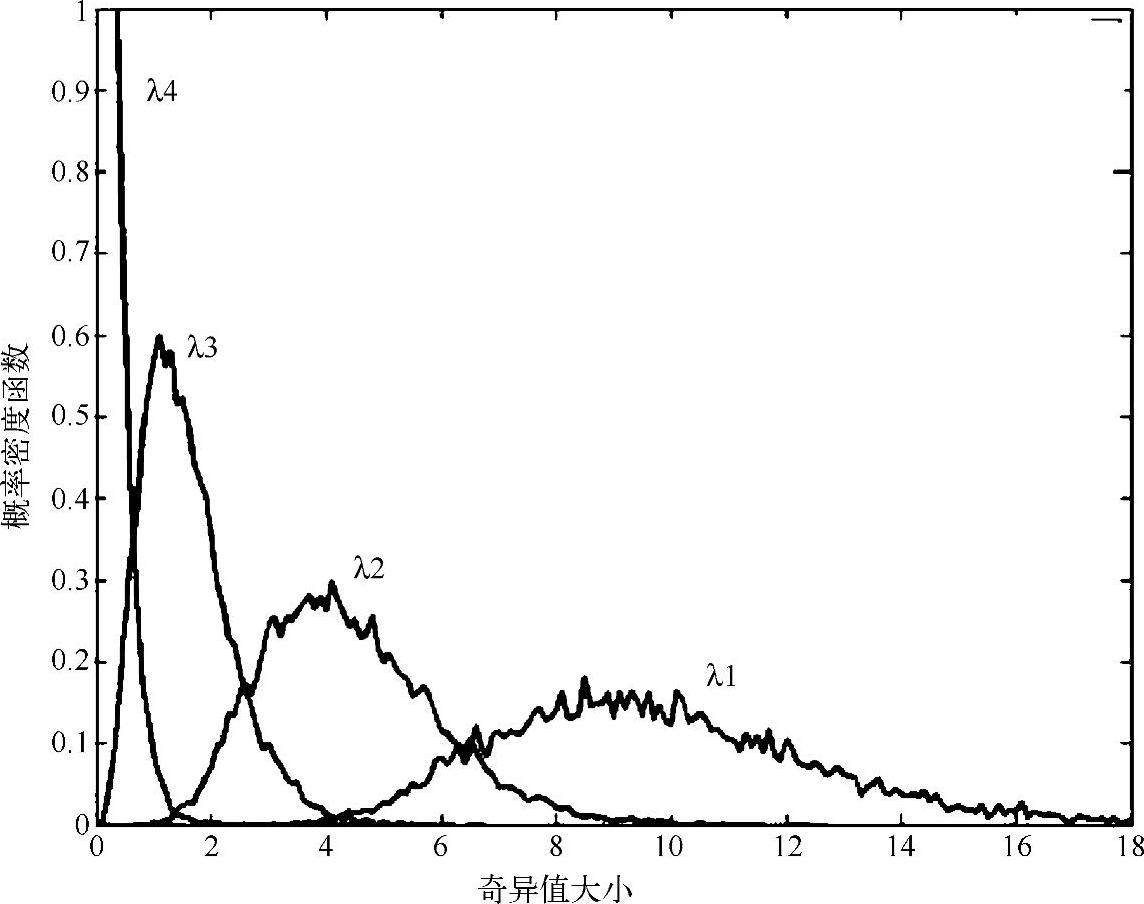
图16-54 ×4信道矩阵各奇异值的概率分布函数

2.SVD分解性质

接下来，我们介绍一些从SVD分解能推导出来的性质，其对应证明见附录E。

性质16-1 对于有t根发射天线，r根接收天线的MIMO信道，记所有t根天线到第i根接收天线的信道衰落系数为h_i=[h_i1，h_i2，…，h_it]，信道矩阵

H=[h^T₁，h₂^T，…，h^T_r]^T=U∑V^H那么，所有t根天线到第i根接收天线的信道衰落系数为

进而有

性质16-2 信道矩阵H所有元素的模与其奇异值之间满足

即信道矩阵的相关矩阵HH^H的迹Tr（HH^H））满足(www.daowen.com)

性质16-3 给定矩阵H=U∑V^H，其奇异值与奇异向量的关系为

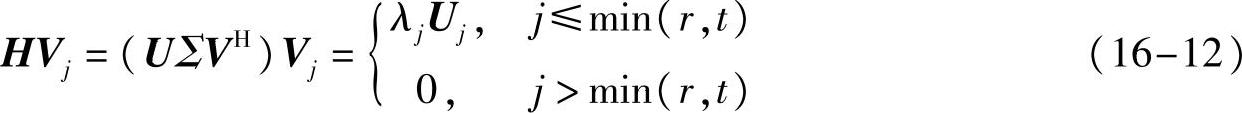
证明 注意U、V都是酉阵，展开即得。

3.EVD分解

除了SVD分解外，矩阵的特征值分解（Eigenvalue Decomposition，EVD）也能派上用场。EVD分解是说，可以把一个方阵A_n×n分解成如下形式：

A=U∑U^H（16-13）

其中，U为n×n酉阵，∑=diag{λ₁，…，λ_n}。记U的列向量表示为

U=[U₁，U₂，…，U_n]

那么有

AU_i=（U∑U^H）U_i=λ_iU_i（16-14）

因此，根据矩阵特征值的定义知，λ_i是矩阵A的一个特征值，其对应特征向量为U_i。

性质16-4 假设信道矩阵H_r×t的SVD分解为

H=U∑V^H

其中，∑=diag{λ₁，…，λ_min{r，t}}_r×t。那么，信道矩阵的相关矩阵HH^H的EVD分解为

HH^H=U∑＇U^H（16-15）

其中，∑＇=∑∑^H=diag{λ²₁，…，λ²_min{r，t}，0…，0}_r×r，表达式中最后连续0的个数为r-min{r，t}。

因为这个性质，在实际应用中，有时SVD分解和EVD分解可以相互转化。比如，当需要信道矩阵的奇异值时，既可以通过对信道矩阵H做SVD分解获得，也可以通过对信道相关矩阵HH^H做EVD分解获得。