为了把空间复用原理理解透，我们再换个角度来描述。假设t行L列预编码矩阵为

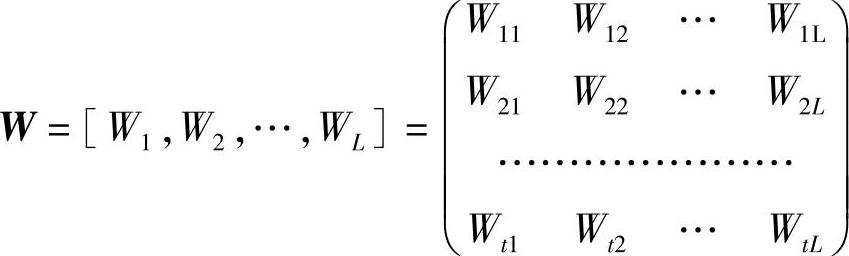
经过预编码后，发射端发射的向量为

WL=x₁W₁+x₂W₂+…+x_LW_L（16-6）

经过信道后接收到的向量是

HWL=x₁[HW₁]+x₂[HW₂]+…+x_L[HW_L]（16-7）

只要式（16-7）中，向量HW_i是无关向量组，那么就可以唯一确定x_i了。图16-4示意了只发送x[ω₁，…，ω_t]^T情况下的MIMO系统。

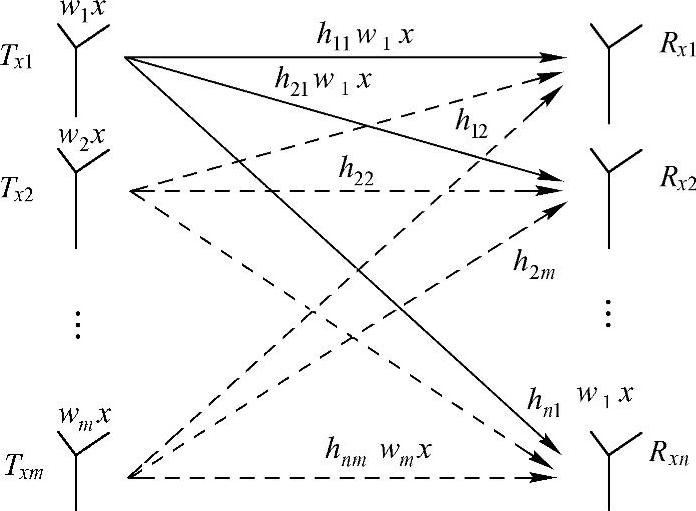
图16-4 MIMO线性处理收发系统

那么，从发射端信号（式（16-6））到接收端信号（式（16-7））的转变，我们看到信道的效果就是把一个t维空间的一个向量（如x_iW_i）变换（映射）到r维空间的一个向量（如x_iHW_i）；如果发射端是把几个向量叠加后发射出去，那么接收端就是相应向量分别被信道作用后得到的向量的叠加。而形式上发射端发射的数据流是携带在发射的各个向量（W_i）上的，那么经过信道后，数据流仍然依附在各向量被信道作用后得到的向量（HW_i）上。因此，我们要从接收到的合成向量中唯一分解出来发射的数据流，那被信道作用后得到的向量必须无关。(www.daowen.com)

知识扩展 上面讲MIMO空分复用流数时，L=[x₁，…，x_L]^T经过W预编码得到Y=WL=[y₁，…，y_t]^T，然后发射出去，接收端收到Z=HY。会不会有人想：只要Y能被唯一解出来，而Y=WL，所以L就能被唯一解出来。所以，对于多重预编码

Z=HABCD…WL

要想唯一解出L，应该要求每一重预编码都是唯一解的，对吗？例如Z=HY，Y必须唯一，而Y=AU，U必须唯一。

事实上，多重预编码的每一重都能唯一解仅是最后一重能唯一解的充分条件，而非必要条件。最简单的例子就是MISO系统，利用预编码向量W发射x，接收端收到z=HWx。想通过Hy=z先解出y再解x是没有办法唯一得到y的。理论原因如下：Hy=z关于y可能有多个解，然而Wx当x遍历所有可能值后，可能只会碰到y的多个解中的一个。所以，虽然单看y有多个解，但把Wx的可能取值情况联合起来看，满足HWx=z的x仍然只有唯一一个。

有兴趣的朋友，也可以考虑一个相关的纯数学问题：线性方程组

A₁A₂…A_nX=Y

关于X有解时，有唯一解的充要条件是什么？其中A_i的维数不一定相同，仅要求满足矩阵乘法，即A_i+1的行数等于A_i的列数。根据上面的讨论，显然所有A_i都列满秩不是充要条件。

三言两语

这里我们没有讨论任何干扰和噪声，各个数据流x_i在目前为止还是平等的地位，没有孰优孰劣。接下来我们加入干扰和噪声等，它们的地位会有一些微妙的变化，注意慢慢体会。