OFDM信号在接收的时候，最理想情况是假设接收端能和一个OFDM符号的第一条到达径精确同步上，然后以第一条径的时间为参考（把接收信号划分成CP部分和有用信号部分），丢掉CP部分，然后把一个OFDM符号除掉CP外的部分拿出来处理或者说从CP结束的地方（有用信号部分开始的地方）开始等间隔采样。所谓时间偏移，主要指CP外部分拿得不准确，或者说采样点采得不准确，相对于上述最理想情况有偏移。从带来的影响来看，我们大致分为两种情况讨论：

●情况A：相对于最理想情况偏移整数个采样点间隔。

●情况B：相对于最理想情况偏移分数个采样点间隔。

而对于其中每一种情况，又可以继续分为三种小情况讨论：

●情况一：第一个采样点比CP结束位置提前。

●情况二：第一个采样点在CP结束位置之后，误差不超过一个采样点。

●情况三：第一个采样点在CP结束位置之后，误差超过一个采样点。

接下来，我们先以整数个采样点偏移（情况A）来讨论其对应的三种情况。

1.情况一

对于情况一，如果CP的长度比时延扩展长，我们再定义一个分界点来讨论，这个分界点是时延扩展最大的结束位置。如果第一个采样点比CP结束位置提前，但仍然落后于时延扩展最大结束位置，我们可以看到每个时延路径上每个子载波的信号仍然是完整的周期，那么正交性没有任何问题。并且对于偏移为整数个采样点来说，得到的采样点是最理想情况采样点的循环移位。比如，最理想情况接收端采样点为[y₀，y₁，…，y_N-1]，满足

其中，x_n为发射端信号；h_l为信道抽头。那么，情况一里偏移k个采样点间隔得到的采样点为

[y₀＇=y_N-k，y₁＇=y_N-k+1，…，yk＇-1=yN_-1，yk＇=y0，…，yN＇-1=yN_-k-1]

记x_n＇为[x₀＇=x_N-k，x_N-k+1，…，x_N-1，x0，…，xN_-k-1]，仍然有

假设最理想情况，DFT到频域得到的平行信道为

Y_n=H_nX_n（15-8）

那么，由DFT的“时域循环移位，频域相位旋转”性质知道，这里偏移情况DFT到频域得到的平行信道为

我们看到，从偏移采样点做DFT出来的对应于每个子载波上的数据除了信道衰落外，每个子载波上还有相位旋转，旋转角度与采样点时间偏移k和每个子载波的频率n有关。(www.daowen.com)

当然，如果接收端仅知道信道衰落系数H_n，但不知道有采样点偏差，即不知道每个子载波上数据有相位旋转，那么解调出来的信号会出错。比如，本来发的是第一象限的QPSK符号，由于相位旋转，解调出来的可能是第二象限的QPSK符号。相反，如果接收端既知道信道衰落系数，又知道各子载波上的相位旋转，那么和采样完全准确时的最理想情况解调没有任何区别。但是这种情况存在吗？或者说合理吗？这种情况要求接收端知道采样偏差是多少，既然知道，那为什么不纠正回去按准确采样点采样处理？既然讨论采样偏差，当然是假设接收端并不知道有采样偏差这回事儿，接收端还乐呵呵地认为采样挺准确的。

然而，如果每个子载波有导频（或称为参考信号）来估计信道衰落，即使接收端不知道有采样偏差这回事儿，但由于对包含导频的OFDM符号来说，它也是有采样偏差的，当然这个偏差接收端也不知道。接收端仍然按正常情况去估计信道衰落系数，估计出的信道衰落系数里，天然会隐含把每个子载波的相位旋转当成信道衰落的一部分，即理想情况下估计出来的信道衰落就是用这个信道衰落系数去解调数据符号，理论上一点问题没有，和正常采样情况效果完全一样，虽然整个过程中接收端仍然不知道有采样偏差这回事儿，但不产生什么问题。不过，有个现实问题可以稍微提一下：现实情况的导频设计可能不是每个子载波上都有，比如LTE里的下行参考信号，它是隔几个子载波插入一个参考信号，这样就不能从参考信号得到每个子载波上的信道衰落系数。一般还需要通过从参考信号得到的衰落系数经过插值方法把其他没有对应导频的子载波的信道衰落系数给估计出来。而当初在设计导频间隔的时候，可能并没有考虑采样时间偏差（或者考虑了一部分范围的偏差），是假设采样准确的情况下来设计的。认为采样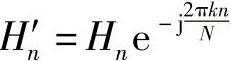准确时，导频足以保证性能。但现在由于采样偏差（或偏差超出预计范围），实际上相当于改变了信道的特征，比如频率选择性增强了，也许还是有些影响，得具体场景具体评估。

如果第一个采样点比最大时延截止位置还提前，显然正交性被破坏。这种情况，只能说理论上一定有影响，但影响到底有多大，纯粹的理论分析不方便给出准确结果。比如，若最大时延路径的功率很微弱，虽然这条径，客观存在，但影响几乎可以忽略不记，也即变相地可以认为最大时延提前了，从而仍然等价于采样点在最大时延截止位置之后，那就属于上一段落讨论的情况；相反，影响就较大了。总之，需要实际情况实际分析。

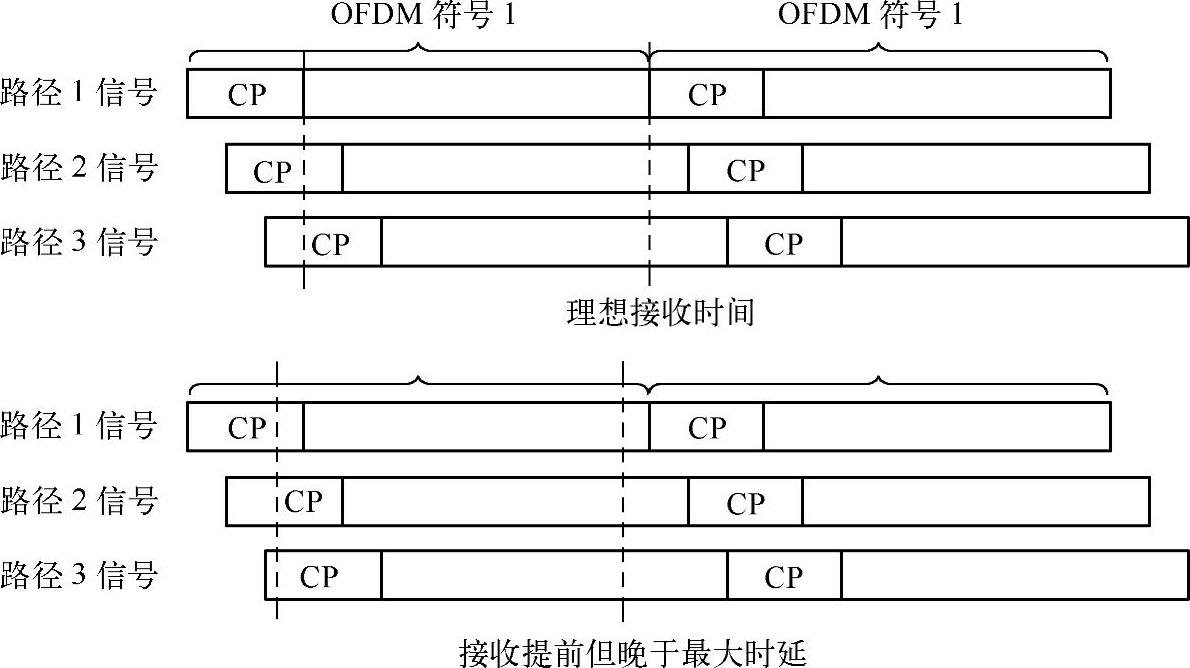
图15-3 时间偏移情况一

2.情况二

对于第二种情况，相对于CP结束位置后有一个采样点偏差。看起来如果按照常规积分解调来说，是应该有正交性破坏的，积分区间都伸到下一个OFDM符号去了。但是，从采样点的DFT来看，对系统的影响仍然只是每个子载波的数据有一个相位旋转而已。因为偏差一个采样点间隔得到的采样点为[y₁，…，y_N-1，y₀]，仍然是最理想情况的循环移位。其他讨论和情况一差不多。并且，因为误差很短，不超过一个采样点间隔，相位旋转角度很小。即使参考信号的估计有误差，误差也很小，一般对系统的影响很小。

3.情况三

对于第三种情况，就比较直观了，不论从常规积分还是DFT/IDFT来看，正交性遭到破坏，总之性能有影响，影响多大要看误差有多大，实际结果需要根据具体场景评估。

经过上面的讨论分析，从整数个采样点时间偏移情况（情况A）来看，情况一和情况二都不会有什么问题。同理，对于分数个采样点间隔偏移（情况B）情况一和情况二也不会有什么问题。下面我们仅看看相对于最理想情况，整数个采样点偏移和分数个采样点偏移的差别。

假设时间偏移为k+子 个采样点，其中0<子<1。回忆我们在无线信道离散模型里讨论信道抽头的影响因素，知道如果有采样偏移，是会改变信道抽头的。那么，记x_N＇为[x＇₀=x_N-k，x_N-k+1，…，x_N-1，x0，…，x_N-k-1]，此时采样点离散传播模型为

但对于OFDM系统，做DFT到频域，仍然能得到平行信道

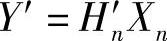
并且H_n＇和H_n之间仍然仅是相位旋转关系，具体地

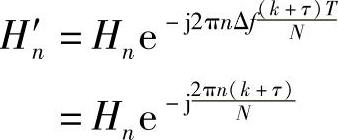
信道抽头h_l＇不再和最理想情况一样。类似地，如果有导频估计信道，那么估计出来的直接就是H_n＇，根本不用去考虑和H_n的关系，照样能正确解调。

最后，现实系统中，一般同步过程不可能达到最理想情况，但从我们的分析可以知道，只要时间偏移最后满足情况一或情况二的要求，理论上就不会有问题。