通过第一部分的介绍，我们知道OFDM技术把数据符号调制在不同的子载波上，例如把数据符号序列[a₀，a₁，…，a_N]分别承载在子载波

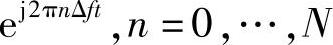
图14-5 增加天线人为制造不同程度延迟

并且并列地发送出去，即发送出去的信号为

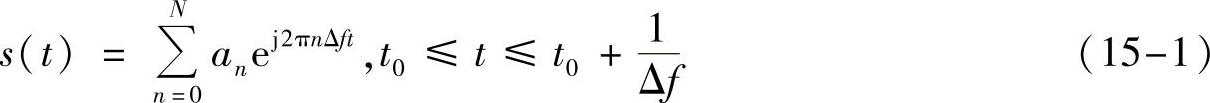
现在的问题是，接收端收到这个整体信号后，怎么把数据符号a_n抽出来呢？提醒一点，接收端当然知道整体信号是上面的和形式，它只是不知道和式中a_n具体是多少。大家想一想，如果存在两个不同的序列[a₀，a₁，…，a_N]，[b₀，b₁，…，b_N]，将其带入式（15-1）得到的信号相同会怎么样？这当然不行，接收端怎么判断到底是发的哪个序列呢？所以式（15-1）和序列一定要一一对应才行，即任何一个信号，只能唯一地表示成式（15-1）的形式。怎么判断式（15-1）一定是唯一的呢？这个原因前面我们已经讲过，因为截断的幂指数函数

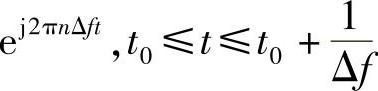
是一组正交基，即

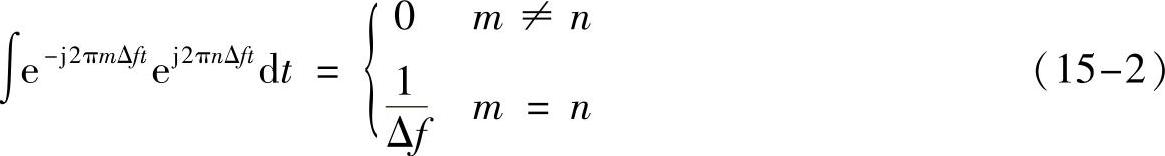
因此，如果一个信号能由它们线性组合表示出来，那么每个基前面的系数（坐标）必然是唯一的。好，现在知道正交了，接收端就好办了，想拿出a_n，只需求每个基下坐标即可

OFDM信号s（t）的时域和频域如图15-1所示，除了时域信号的正交性由积分表示出来之外，其正交性还可以从频域体现出来。

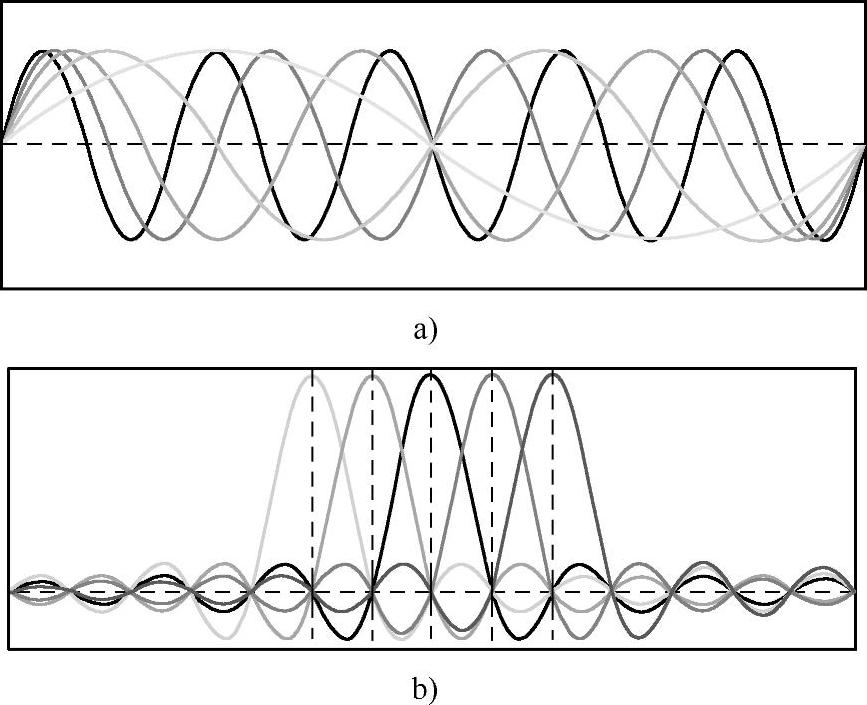
图15-1 OFDM时域与频域信号

a）信号时域 b）信号频域(www.daowen.com)

从上面我们可以看出，数据符号即使是给不同用户的也可以，只要分别告知用户他们的数据在哪些子载波上即可。换言之，OFDM还可以被用来作为一种不同用户的复用多址技术，即OFDMA。

进一步研究，我们发现发射端信号的生成可以借助对待发射序列[a₀，…，a_N]应用IDFT变换来先生成采样点，再通过数/模转换得到；而接收端可以通过对接收信号采样再做DFT变换来得到发射的序列。这样大大简化了OFDM技术的实现，从而获得广泛的应用。

通常我们认为一些经典知识都是很早就有的，比如牛顿时期。不过告诉大家，DFT简化┈的推导看起来很简单，实际上这个技巧在1971年左右才被发现，牛顿也许并不知道。┈

相应地，OFDM技术也被这样描述：把要传输的数据先串并变换，然后IDFT，接着经过信道，再DFT，最后解调。

这样描述其实有那么一丁点误导之闲，给人感觉发射端和接收端就是一对IDFT/DFT互逆操作，真的是吗？如果真的是，这和映射到正交的子载波上有什么关系？似乎没什么关系。我只要把IDFT出来的数据当成一个个脉冲发送出去就行了，即使不是OFDM系统，我也可以这样做。似乎没什么不对？确实也没什么不对，原理上也是绝对正确的。那OFDM技术的意义是什么呢？

下面，我们看看OFDM技术有意义的地方。上面的分析中，我们只从时间纬度，逻辑上来看待这个问题了，确实逻辑理论上完全没发现OFDM的特别之处。其实，OFDM的初衷是有比较高的频谱利用效率。我们在研究无失真传输的时候就已经讲过，有很多信号的采样序列可能是一样的，但是这些信号本身的频谱可能千差万别，有些频谱宽，有些频谱窄。这里也是一样。确实只要想办法把IDFT得到的数据发送出去，接收端能得到这个序列即可。关键是选一个什么样的信号把这串序列携带出去呢？这才是OFDM技术能发挥作用的关键。对于OFDM技术，不管怎么选，最后发送出去的信号要尽量像下面这个信号：

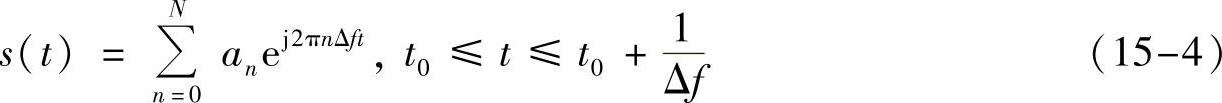
这样可以保证频谱利用率较高。

通常在通信系统基带表示中，喜欢把OFDM的子载波摆成正/负频率基本对称的形式，即

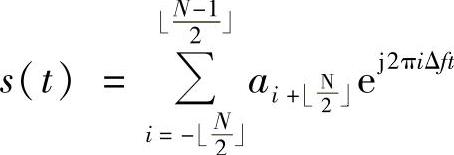
在这个形式下讨论发射端IDFT和接收端DFT时，有一点小区别，请大家注意。对这种形式基带信号采样，其N个采样点为

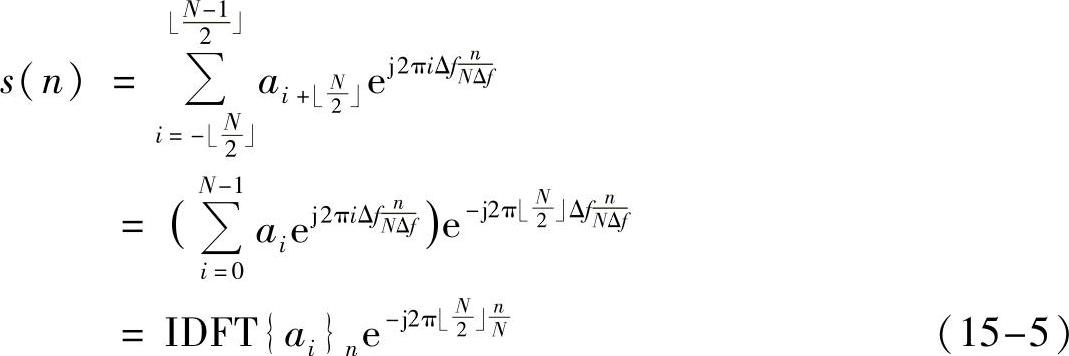
即相对于序列a_i（0≤i≤N-1）的IDFT有一个相位旋转。同样，接收端在用接收到的采样点做DFT还原a_i时，可以先把所有点上的相位旋转去掉然后再做DFT；或者，由于时域相位旋转对应到频域循环移位，那么接收端可以直接做DFT，然后循环移位还原也可以得到a_i。

总之，有一点小区别，但都不是大问题，后续讨论时，如果没有特别需求，我们还是采用比较正常的形式方便点。