如上所述，时间分集就是在多个信道不同的时间上发送信号。我们谈到分集思想，需要明确是对哪个对象应用了分集思想，或者说哪个对象能够获得分集增益，这个必须搞清楚。通常在无线通信里，大致可以分为两种情况来讨论，其他情况思想类似。这两种情况分别是：对单个数据符号应用分集思想和对单个编码块应用分集思想。

先讲对单个数据符号应用分集思想。对单个数据符号应用时间分集，就是在多个信道不同的时间上发送相同的信号。比如，假设信道传播模型是

y=hx+w

同一个数据符号X发送L次，其中第i（1≤i≤L）次接收到的是

y_i=h_ix+w_i

首先说，不论h_i之间的关系怎么样，多次发送错误概率一定是降低的。因为多次发送时，只要其中有一次正确就应该认为是正确的；而所谓错误，要所有次数全部错误才算错误。假设每次发送是独立判决的，多次发送的整体错误概率是单次发送错误概率的乘积，显然比单次的错误概率小。但是，我们上面说了有增益并不代表是分集增益。下面我们讨论时间上重复发送在哪些情况获得的增益才是所谓“分集增益”。

1.多次发送信道衰落完全相同

不论是慢衰落还是快衰落，假设多次信道衰落完全相同，都为h，采用MRC合并后，有

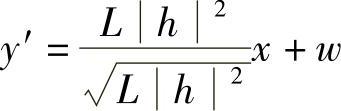
其接收SNR相对于单次发送总是提高L倍，不论h是多少。也就是说，不论h是慢衰落，还是快衰落，多次发送的效果，通过单次发送但发射功率提高L倍也能达到。注意到时间多次发送和多天线SIMO系统，时间单次发送和SISO系统没什么区别。为了简便叙述，我们就用SIMO系统和SISO系统来分别指代。也就是说，SIMO系统相对于SISO系统有10lgL（dB）增益。特别地，当L=2时，有10lg 2=3 dB增益。但是这种情况如我们前面的讨论，既然单次也能达到相同的性能，这个增益并不是“分集”增益，这个增益一般称为“功率合并增益”或者“阵列增益”。

2.多次发送信道是独立快衰落

假设多次信道衰落是相互独立的，并且假设每一次都是快衰落，分别为h_i，采用MRC合并后，有

则对于每一组信道取值[h₁，…，h_l]，采用MRC后信号的接收SNR为

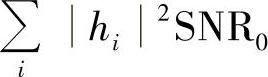
其中，原始信噪比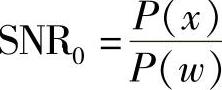。以信号取值x=a或x=-a且等概率出现为例，以式（14-29）为基础，通过先验概率计算得条件误码率为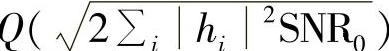。其中，

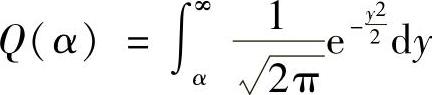(www.daowen.com)

且注意，所有满足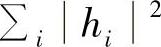相等的信道MRC后，接收SNR相等，从而该条件误码率相等，都为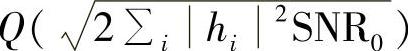。现在，假设随机变量Y=∑_i|h_i|²的概率密度函数为f（y）。那么，可以得到该SIMO系统MRC下的平均误码率为

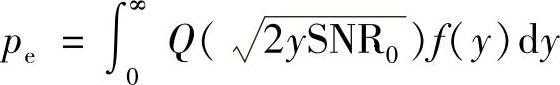
从性能上来说，每次发送时信道相互独立的SIMO系统采用MRC能够同时提供功率合并增益和分集增益。图14-2示意了不同接收天线个数的SIMO系统采用MRC的平均误码率。

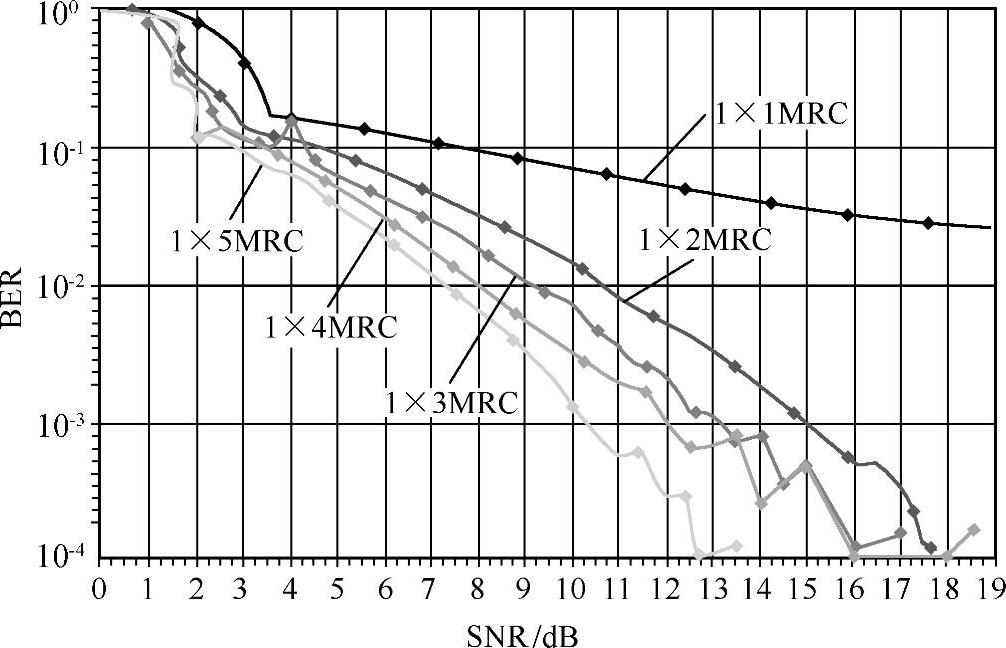
图14-2 不同发送次数时MRC接收

从图中我们看到，1发2收的SIMO系统大概在SNR为4.5 dB时达到10%的误比特率（BER），而SISO系统大概在SNR为8 dB时达到10%的误比特率，即1发2收SIMO系统MRC相对于SISO有3～4 dB增益。而如果两次发送信道完全相同，前面讲过理论上只有3 dB增益。另一方面，我们知道多次发送的平均信号接收功率为

即统计平均来看，每次发送信道独立时，MRC合并也使得合并后SNR只平均增大L倍。但我们却看到增益更大，这个多出来的增益就是分集的功劳。

另一方面，从错误概率（瀑布）曲线来说，一个方案的分集增益体现为对应曲线随着原始SNR的斜率变化情况。但从图14-2可以发现，随着发送次数的增多，每增多发送次数时带来的增益也逐渐减小，并且BER曲线随着天线数的增多越来越趋近于平移（平行）关系，其陡峭程度（斜率）不再变化，这又是为什么呢？原因是，分集增益的实质是改变了接收功率的概率密度分布。例如，如果每根接收天线的信道衰落都是相互独立的瑞利衰落，当有L根接收天线时，接收信号功率∑_ih_i²满足2L阶χ²分布。图14-3给出了不同阶数k时的χ²分布。

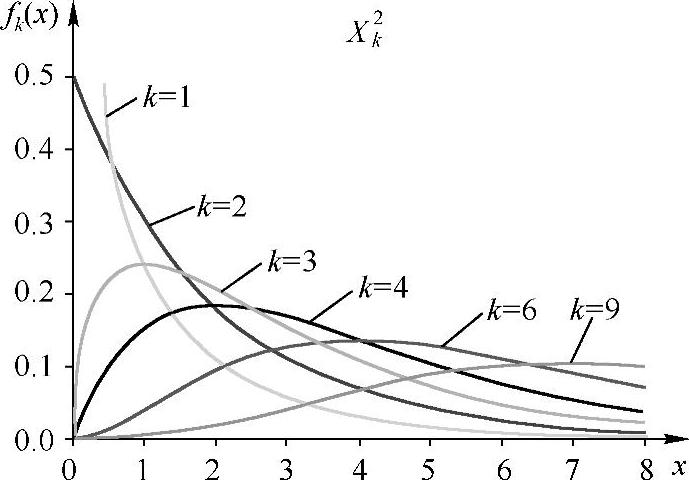
图14-3 不同阶数的χ²分布概率密度

但是，当独立的信道个数N足够大时，根据中心极限定理，其（归一化）接收信号功率

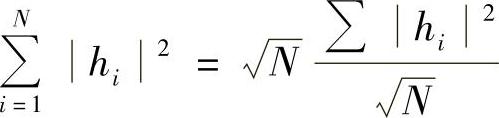
将趋近于高斯分布（正态分布），如图14-3中，当k=9时，分布曲线已经开始像高斯分布了，那么仅仅只剩下分布的方差会随着天线个数增加而变化。所以，当信道大于一定个数时，即接收天线个数达到一定数量时，不再有增加的分集增益，仅剩下功率合并增益，表现为BER曲线越来越平行。

再者，有可能存在k，使得功率提高k倍但采用单次发送来达到相同平均误码率吗？没这个可能！因为∑_ih_i²满足2L阶χ²分布，而对于任意k，kh₁²满足2阶χ²分布，错误概率变化趋势不会一样。因此，按照我们对分集的认识，多天线信道独立时一定有分集增益。

上面讲了对单个数据符号应用分集思想，下面介绍对一个编码块应用分集思想。假设一个编码块包含数据符号[x₁，…，x_N]。如果这些数据符号经历的信道衰落完全相同，比如在相干时间内，如果信道好则所有数据符号都好，信道如果差则所有数据符号都差。然而，如果这些数据符号经历的信道衰落独立分布，虽然从单个数据符号来看，每个符号反正只发了一次，无所谓是否有分集增益，但是从整个编码块来看，每个符号经历的信道是独立的，有些好有些坏，最后长期来看会获得平均的效果，从而提升性能。也就是把整个编码块当成一个整体来看，获得了分集增益。因此，我们谈到分集增益，先要看讨论的对象是谁。