上面讨论的几种接收算法（均衡算法）都是不去改动信号发射机制，直接实打实地去均衡，并且都可以看成在时域做均衡。有没有办法通过对发射机制改动一下，使得均衡变简单呢？我们看到ISI信道

形式上基本上快变成循环卷积啦，特别是当i≥L时。如果是循环卷积的形式的话，我们知道通过DFT变换可以变成乘积形式，乘积总比卷积看起来简单。那我们就想办法先凑个循环卷积形式出来吧。

要想使得从0≤i<L起就是卷积形式，即要

观察知，如果发射端发送的是

接收到的是[y_-L+1，y_-L+2，…，y0，y1，…，yN_-1]，则

从而对于

有如下循环卷积关系：

这种得到循环卷积的方法里，在x₀之前额外发的信号称为循环前缀（Cyclic Prefix，CP）。对式（14-25）采用DFT变形，得到(www.daowen.com)

DFT{y}=DFT{h}DFT{x}+DFT{w}（14-26）

分开写有

Y_i=H_iX_i+W_i（14-27）这样，把时域的多径信道变成了频域平行信道，当然要付出CP的代价。接收端可以对每个平行信道单独检测，把X_i都判决出来后，再用IDFT把x_i还原出来。

我们在刚开始提到从频域看ISI信道时就说过，不管是否加CP，DFT变到频域来看为

那么总是可以写成

其中，DFT{x[n]}_i表示序列x[n]的DFT对应的第i个分量。h^_i有什么规律可循吗？如上面讲的，如果加上CP，那么h^_i和h_i满足DFT关系

完全由信道决定，和发的信号x_i没有任何关系；而如果不加CP，虽然从频域看也可以写成平行信道，但是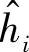不仅和信道h_i有关，还和当前发的信号x_i的取值相关，那基本上没办法相干解调了，因为要知道频域信道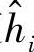，需要先知道时域信道抽头h_i和发射的信号x_i才能均衡解调x_i，这就像“鸡生蛋，还是蛋生鸡”问题一样。当然对于不加CP的频域均衡也有很多研究成果，但稍微复杂一些，这里就不做介绍了。