假设信号X经过信道后，得到

Y=HX+Z+W （14-22）

其中Z为干扰，W为噪声。仍然只考虑线性接收，即仍然考虑把接收信号往某个方向投影。首先说，采用MRC还好吗？上面我们讲了噪声W往哪个方向投都无所谓，但是干扰Z不一定有这么好的性质。采用MRC是把接收信号往信号方向投影，虽然信号投影长度能达到最大，但是如果Z和信号相关度较高（即方向差不多），Z的投影可能也很大，所以最后整体性能可能不好。那我们换个思路，干脆把接收信号投到与Z正交的方向上，这样即采用ZF把Z完全消掉（投影为0），岂不是感觉很好。打住，也许没你想象的好，和上面一样，虽然Z投影变为0了，可能信号部分的投影也几乎变为0了，而还有个家伙噪声W没变，最后性能也不会好。

三言两语

这样一想，我们大概知道了思考的方向：存在一个方向，虽然信号投影不像投到信号自己方向上那样大，即有所减少，但Z在那个方向上减少得更快，从而整体性能可能还不错。也即存在一个方向，可以最大化信干噪比（SignaltoInterference-NoiseRatio，SINR），使得干扰和噪声两者都能照顾到。

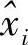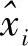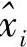上面比较中庸的思想引出线性最小均方误差（Linear Minimum Mean Square Error，LMMSE）算法。长期来看X，Z，W为随机向量，当然Y也是一个随机向量，但Y是由随机向量X，Z，W组合而成的随机向量，即它们的函数。现在要以观察到的随机变量Y为基础，找一个随机变量，使得该随机变量与真实_i的平均距离长期统计最小，即平均误差最小。也就是说，以时刻1观察到的Y₁为基础，找一个，求该与时刻1本来发送的x_i的距离；以时刻2观察到的Y₂为基础，找一个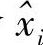，求该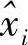与时刻2本来发送的x_i的距离；一直这样考察下去，最后使得找的序列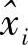与实际发送的序列x_i的距离平均最小。

上面说了以观察到的随机变量Y为基础来找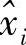，但是没有说应该以什么方法或者规则来使用Y。一个比较简单且常用的规则就是采用Y的分量y_i的线性表示（注意y_j长期看是随机变量），即使得找到的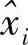形如

也就是说，要找到一组常数g_ij（注意不是随机变量）使得上面形式的数与实际发送的x_i统计距离最小，或者叫统计误差最小。

我们可以按照线性空间的条款验证一下，对所有可能的常数g_ij，对应得到的

构成一个线性空间（其中元素是随机变量）。上面的描述，其实是说，在该线性空间中找一个随机变量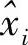使得它与随机变量x_i的距离最小，即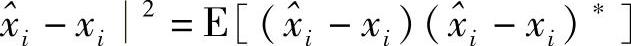最小，也就是说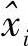是x_i的最佳近似。

则根据附录B里讲的正交原理（Orthogonal Principle）知，该

必然满足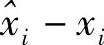与如上考察的线性空间中任何向量正交。因为所有y_j也在该线性空间内，所以必然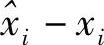与所有y_j（1≤j≤r）正交，即

根据随机变量内积定义展开有(www.daowen.com)

继续展开可求出所有g_ij的值，这里略去细节。这里可以有更直接的方式，即把所有x_i对应的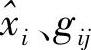一起考虑写成矩阵、向量形式：求X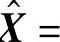，使得它与X的距离最小，其中G为所有g_ij组成的矩阵。设

则<GY-X，Y>=0从而

GE[YY^H]-E[XY^H]=0

那么，可以得到

G=E[XY^H]E[YY^H]^-1=H^H（HH^H+E_s^-1R+E_s^-1σ²I）-1（14-24）

其中，

●E[XX^H]=E_sI，E_s为X每个分量的功率。

●E[WW^H]=σ²I，σ²为噪声功率。

●E[ZZ^H]=R为干扰协方差矩阵。

因为ISI信道传播模型可以写成

y=Hx+w

LMMSE均衡也可直接应用与ISI信道，不细讲了。