首先，我们看看两个直观而又合理的判断原则：在接收到的数据的条件下，这个接收数据最有可能是因为发射端发射哪个信号造成的，就认为发射端发射的是哪个信号，这个可能性称为后验概率，这个判断准则就是根据接收到的数据，判断成后验概率最大的发射端可能信号；或者看发射端发射哪个信号，经过信道后出现接收到数据的概率大，这个条件概率称为先验概率，也即选择经过信道最有可能得到当前观察值的候选信号。事实上，我们在本书第二部分已经讲过AWGN下的先验判决和后验概率判决，其中的先验概率判决也称为最大似然接收（Maximum Likelihood，ML）。这里我们以SIMO信道模型为例，再简单回顾一遍。假设SIMO信道模型里有r根接收天线，

y_i=h_ix+w_i

其中，h_i为发射天线到接收天线i的信道衰落系数，各ω_i～CN（0，σ²）且相互独立。假设接收端可以准确地知道各信道衰落系数，则根据ML准则，判决结果应该为

其中，x_i遍历所有发射端可能发送的信号。另一方面，把SIMO过程还是分成两个阶段来看，第一个阶段是无误传输

x→h_ix

第二阶段分别叠加噪声w_i，相当于在AWGN信道发射了r个信号h_ix。那么，我们只需要采取就近判决（向量形式下）就相当于ML判决，这个和式（14-10）表示的结果一致。

对于离散信道模型，发射端发送x=[x（0），…，x（N-1）]，接收端接收到y，在相干时间内满足

其中，w（n）为相互独立的噪声。当L>1时，我们称之为有码间串扰（ISI）信道模型。对于ISI信道模型，假设接收端知道信道抽头h_l，我们也可以应用ML算法，即计算所有候选序列x的先验概率，然后选择先验概率最大的作为判决结果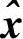。那么，

注意到，当x（0），x（1），…，x（N-1）给定时，y（i）发生的概率仅由w（i）决定，即y（i）之间相互独立，从而有(www.daowen.com)

我们取个对数把乘法变成加法吧，则式（14-13）等价于

假设每个数据符号x（i）的可能取值个数为M个，那么长度为N的候选序列x共有M^N个，对于每一个x取值需要计算N个y（i）的条件概率，也即总共要计算NM^N次概率。当N很大时，这个指数增长的计算量会很大。能把计算量降下来吗？继续注意到，其实y（i）最多只与L个x（j）有关，即与[x（i-L+1），…，x（i）]有关，而不是和序列x的所有N个分量相关，那么式（14-14）可进一步化简成

-log prob{y（i）[x（i-L+1），…，x（i）]}

计算出来摆在那儿，这个过程共需要计算M^LN次条件概率。第二步，就是利用计算出来的条件概率来组合搜索出“和概率”最小的候选信号序列x。我们先定义N个步骤，步骤i里有M^L个状态，即可能的[x（i-L+1），…，x（i）]的取值，步骤i+1里也有M^L个状态，即可能的[x（i-L+2），…，x（i+1）]的取值。如果步骤i+1里的是一个状态序列的前L-1个分量，与步骤i里某个状态的后L-1个分量相同，称具有这种关系的步骤i+1里的这样的状态为相应步骤i里的状态能够到达的状态。那么从步骤0的一个状态可以到达步骤1的一个状态，步骤1的这个状态可以到达步骤2里的一个状态，依次类推，最后到达步骤N-1的某个状态。我们把这些可到达状态的连接称为一条路径，可以看到一条路径其实对应于一个候选序列x。式（14-15）的意思就是从步骤0的某个状态[x（0），…，x（L-1）]到达步骤N-1的某个状态[x（N-L），…，x（N-1）]的路径里经过的所有状态，其中第i个状态给了一个权重

-log₂prob{y（i）[x（i-L+1），…，x（i）]}

然后计算整条路径上所有状态的权重之和，最后找出重量（权重之和）最小的那条路径。找到这个最短路径的有效方法就是所谓的维特比（Viterbi）算法了。

当然，上面描述了先把所有先验概率（权重）计算出来，然后再搜索重量最小路径。实际算法中可以一边计算权重，一边搜索。当L远小于N时，其复杂度远小于式（14-14）对应的穷举搜索。当然当L≈N时，该算法就没什么优势了。注意到上面要解决问题的特征，也即ISI信道模型的特征，是每一个观察值只与部分原数据相关，从而可以利用Viterbi算法进行最大似然算法的化简。另一个应用Viterbi算法的例子就是卷积码的译码啦，因为它也很符合这个特征，即每个码字比特只与部分信息比特相关，而非与整个参与编码的信息比特相关，其具体内容请大家查阅资料了解。