前面的讨论都是基于发射端只有一根天线、接收端只有一根天线(通常称为SISO)的情形,接下来我们讨论一下简单的多天线模型。首先讨论发射端有一根天线,接收端有r根天线的情形。假设发射端发射的是x,每根接收天线接收到的分别是
yi=hix+wi
其中,hi为发射天线到第i根接收天线的衰落系数,wi~CN(0,σ2)且相互独立。接下来,SI- MO信道模型下也可以像SISO信道模型下一样分为三种情况:固定慢衰落、随机慢衰落和快衰落。
1.固定慢衰落SIMO信道
假设每个信道衰落系数hi是固定的,且为收发两端所知。现在假设各天线中h0最大,那么只看y0,这就是一个简单的固定慢衰落信道,其容量为
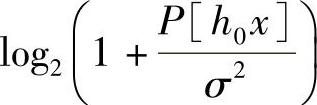
能利用其他天线进一步提高容量吗?应该是可以的。这里,我们假设采用线性合并各接收天线的接收数据来看看有什么收获。所谓线性合并,就是各接收天线接收到的数据的加权求和。假设接收天线i的加权因子为h^i,则合并后得到
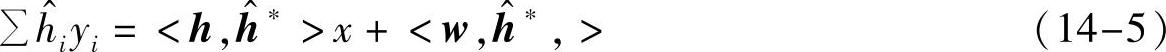
其中,
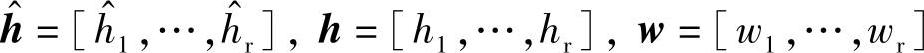
式中,<,>表示向量间最常用内积运算。可以看到合并后等价得到一个SISO固定慢衰落信道。对于给定的合并系数h^i,合并后信道的接收SNR为
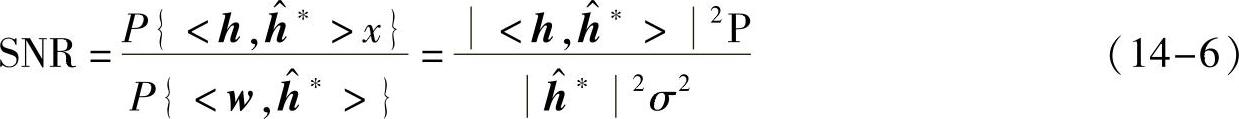
那么该合并方式能达到的信道容量就为
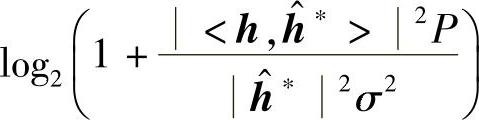
显然,对于不同的合并系数,能确定的信道容量不同。那么请问当合并系数为哪种情况时,确定的信道容量最大?显然只要合并后SNR最大就行了,即要(https://www.daowen.com)

最大化。根据Cauchy-Schwarz不等式,有
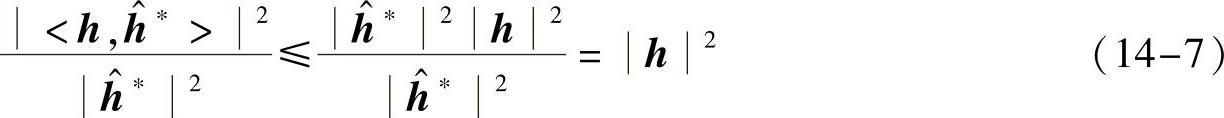
其中,当且仅当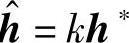 时,达到最大值。也就是说按h^=kh来进行合并,能使得合并后SNR最大,这种合并方式称为最大比合并(Maximum Ratio Combining,MRC)。通常取k=1/h来归一化合并系数,即
时,达到最大值。也就是说按h^=kh来进行合并,能使得合并后SNR最大,这种合并方式称为最大比合并(Maximum Ratio Combining,MRC)。通常取k=1/h来归一化合并系数,即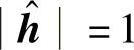 。那么可以看到,线性合并能达到的最大信道容量为
。那么可以看到,线性合并能达到的最大信道容量为
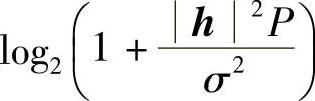
把整个过程联系起来看,要达到该最大信道容量,首先发射端按照信号功率为h2P、噪声功率为σ2的AWGN把最大个数能相互区分的信号y'都挑出来,然后实际发送信号y'/h即可(注意实际发送信号的功率为P{y'}/h2=P)。请大家自行跟踪接下来按照归一化的MRC合并是什么样子。最后,显然接收天线数r越多,能达到的信道容量越大。
2.SIMO随机慢衰落与快衰落
SIMO随机慢衰落和SISO随机慢衰落类似,各个信道hi也是一锤子买卖,但接收端不知道这“一锤子”砸在哪儿,所以也没有确定的信道容量,能讨论的也就是溢出容量和溢出概率。如果接收端仍然采用MRC,那么很容易知道溢出概率prob(R)为
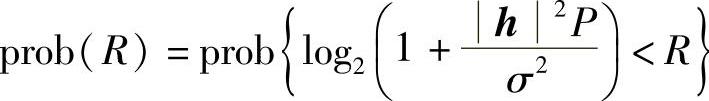
溢出容量就是溢出概率的逆函数。由于接收天线数越多,本来能达到的信道容量越大,那么对于给定的概率,接收天线数越多,对应的溢出容量越大。图14-1示意了不同接收天线数对应概率为10%的溢出容量,可以看到相同原始SNR时,接收天线数越多,溢出容量越大。

图14-1 SIMO场景里概率为10%时的溢出容量
同样,SIMO快衰落和SISO快衰落类似,有确定的遍历容量,若接收端采用MRC合并,遍历容量具体为
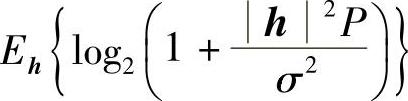
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






