4.3.3.1 设备整体计算及受力分析

1）设备整体重量计算

通过预先的设计参数，抛石管保持架的总重量在22 t左右，建模后通过Solidworks称重发现，并没有达到预先设定的重量，实际重量大约为14 t，考虑焊接的焊缝，以及固锁在保持架装置上的抛石管和抛石整平头，为了结构设计的安全性考虑，其设备重量定为15 t进行后期计算，则整套设备重为15 t。

抛石管保持架滑轮底座处给的力需要大致与保持架自重相持平，所以定滑轮上所带的垂直向上的力为15 t。

2）保持架工况下各位置所受载荷计算

由于保持架下方的滑轮提供的力大致可以抵消保持架自身的重力，另外基本不存在垂直方向的力，所以在此不考虑垂直方向的载荷，优先计算水平方向的载荷。

在抛石整平头进行整平基面时，可以通过保持架的受力情况进行分析。如图4-74所示，抛石管所受的基面摩擦力为F C；抛石管底部（包含抛石整平头）到水面的范围受到一个水流对抛石管运行的阻力F w；因为抛石管与保持架接触的只有两对耐磨板（其中一对耐磨板包含两块相同的且对称布置的耐磨板），且该情况也不太适用超静定计算结构内力，所以本情况视为静定梁静定力学分析，其中A点和B点两个铰点即代表保持架上两组耐磨板的位置；保持架工况时翻转机构的旋转轴d-d给保持架提供约束；其固定机构中也有小销轴连接在保持架上给保持架提供约束。图4-74为抛石管保持架的受力分析。

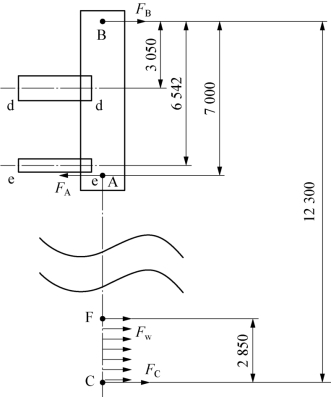
图4-74　抛石管保持架受力分析

波浪力计算，通过查找资料可知，波浪力F w的计算与水中接触面面积、水流速度等因素有关，可以通过式（4-13）计算：

式中，C d为拖拽力系数；v为最大工作流速（m/s）；ρ为水密度（kg/m3）；A为研究对象在水中的横截面面积。

由此可计算抛石管在水中受到的水流波浪力，其中最大工作流速v=0.5 m/s，水密度ρ=1×103 kg/m3，通过式（4-13）计算可得

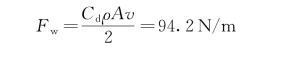
抛石管工作时横向水平力计算，由企业项目基本参数可确定抛石管工作时受到水平横向力大小为2 t，可以计算抛石管保持架中受力分析图4-74中F C的大小，其中取重力加速度为g=9.8 m/s2，通过下式计算可得

F C=mg=2×103 kg×9.8 m/s2=19600 N

因为抛石管与保持架接触的只有两对耐磨板（其中一对耐磨板包含两块相同的且对称布置的耐磨板），且该情况也不太适用超静定计算结构内力，所以本情况视为静定梁静定力学分析，其中A点和B点两个铰点即代表保持架上两组耐磨板的位置，其中d-d、e-e的两个约束实际工况下并不参与其受力，在此可忽略，则静定梁受力分析图如图4-75所示。

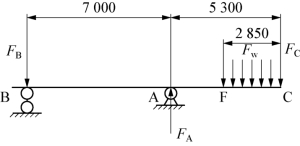
图4-75　静定梁受力分析图

由此可以建立剪力和弯矩的平衡方程，可以通过剪力平衡公式（4-14）和弯矩平衡公式（4-15）计算：

由此可计算A、B点处的约束力，其中F w=94.2 N/m，F C=19600 N，CF=2850mm=2.85 m。其中各力的大小关系为

则可得F A≈34.8571 k N，F B≈14.9886 k N。

由于F A和F B均分别由两块对称且相同的耐磨板承受，所以

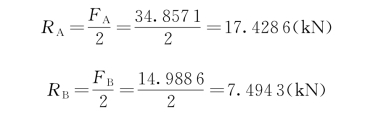
绘制其剪力图和弯矩图分别如图4-76、图4-77所示。

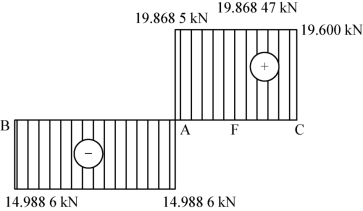
图4-76　剪力图（一）

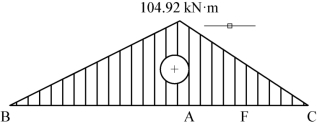
图4-77　弯矩图（一）

4.3.3.2 保持架水平固定时各位置受力分析

当翻转机构旋转轴带动抛石管保持架旋转90°至水平状态时，保持架水平固定时，此时保持架仅受自身重力（包含抛石管和抛石整平头）以及保持架侧面滑轮所安装的钢丝绳上所提供的竖直方向的力。此时抛石整平头上翻转机构及固定机构上的大小销轴也固定在抛石管保持架上，实际情况下不受力，但是作为两个约束存在。

通过企业项目的设计参数可知，保持架在水平固定时的重心（包含抛石整平头、抛石管）处于距离旋转中心靠近保持架顶部方向的0.6 m，其重量（包含抛石整平头和抛石管）大约为52 t。其中，取重力加速度为g=9.8 m/s2可以通过下式计算其所受重力大小为则水平状态下静定梁受力分析图如图4-78所示。

G=mg=52×103 kg×9.8 m/s2=509.6 k N

由此可以建立剪力和弯矩的平衡方程，可以通过剪力平衡公式和弯矩平衡公式计算。由此可计算A、B点处的约束力，其中，G=509.6 k N。其中各力的大小关系为

图4-78　静定梁受力分析图

∑F Y=F 1+F 2-G=0(www.daowen.com)

∑M 1=F 2×4.614-G×0.15=0

则可得F 1≈491.24 k N，F 2≈18.36 k N。

绘制其剪力图和弯矩图分别如图4-79、图4-80所示。

图4-79　剪力图（二）

图4-80　弯矩图（二）

4.3.3.3 上箱梁截面工况下正应力计算

前面计算了保持架整体及各个截面所受剪力及弯矩，并通过计算得出了其剪力图及弯矩图。但是最终还要对抛石管保持架进行强度计算，必须确定保持架横截面上的应力，即需要确定抛石管保持架危险横截面上的应力，即确定研究对象横截面上的最大应力值和应力分布情况，因为构件的破坏一般开始于危险截面应力最大的地方。所以在此选择了保持架上较为危险的上箱梁截面进行正应力的计算。因此，研究保持架受力时横截面上应力分布规则，确定应力的计算公式，是计算研究对象强度必须要解决的问题。下面将分别计算上箱梁截面的惯性矩和上箱梁截面处所受的弯矩大小。

上箱梁的横截面是由多个简单图形组合而成，对于这种组合截面，需要用组合法计算它的惯性矩。即在这里把该组合截面划分成n个简单图形，设每个简单图形的面积分别为A 1、A 2、…、A n。根据惯性矩定义及积分的概念，组合截面对某一轴的惯性矩等于每一简单图形对同一轴的惯性矩之和，计算公式如下：

根据平行移轴定理可知，截面对任一轴（不通过形心）的惯性矩，等于截面对平行于该轴的形心轴的惯性矩与一附加项之和，该附加项等同于截面面积与两轴距离平方之积，计算公式如下：

1）上箱梁截面组合截面惯性矩计算

根据上箱梁截面图，将上箱梁的截面分割为27个简单图形，其各个简单截面均为规则的矩形，其坐标系中该组合截面的形心坐标可通过第2章中Solidworks整体建模获得，通过软件的计算可知，其形心C的坐标为（337，-94）。

由平行移轴定理公式可计算得到上箱梁截面各分割块对同一轴的惯性矩，而组合截面（即上箱梁截面）对该轴的惯性矩等于各分割块对该轴的惯性矩之和，所以，由惯性矩的组合公式计算可得

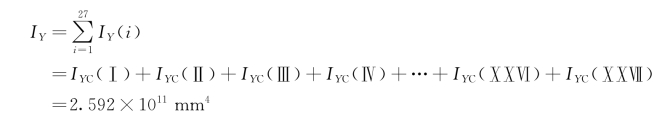
2）上箱梁截面工况下弯矩计算

当抛石管保持架处于工作状态下，根据抛石管保持架静定梁受力分析图4-75及抛石管保持架弯矩图4-77，可得上箱梁截面受到的绝对值最大弯矩时最大弯矩为39.45 k N·m。

3）上箱梁截面工况下正应力计算

通过查找资料可知，横截面任意一点的正应力σ计算公式如下：

式中，M为该横截面所受的弯矩大小（N·m）；y为该点关于中性层的距离；I为截面对中性轴的惯性矩，其大小只和截面形状及尺寸有关。

由正应力计算公式计算可得

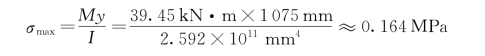
此时其所受正应力远远小于Q345D钢材的许用正应力。

4.3.3.4 下箱梁截面工况下正应力计算

下面将分别计算下箱梁截面的惯性矩和下箱梁截面处所受的弯矩大小。

下箱梁的横截面是由多个简单图形组合而成，对于这种组合截面，需要用组合法计算它的惯性矩。即在这里把该组合截面划分成n个简单图形，设每个简单图形的面积分别为A 1、A 2、…、A n。根据惯性矩定义及积分的概念，组合截面对某一轴的惯性矩等于每一简单图形对同一轴的惯性矩之和。

根据平行移轴定理可知，截面对任一轴（不通过形心）的惯性矩，等于截面对平行于该轴的形心轴的惯性矩与一附加项之和，该附加项等同于截面面积与两轴距离平方之积。

根据下箱梁截面图，将下箱梁的截面分割为22个简单图形，其各个简单截面均为规则的矩形，其坐标系中该组合截面的形心坐标可通过Solidworks整体建模获得，通过软件的计算可知，其形心C的坐标为（337，-94）。

由平行移轴定理公式可计算得到下箱梁截面各分割块对形心轴的惯性矩，而组合截面（即下箱梁截面）对该轴的惯性矩等于各分割块对该轴的惯性矩之和，所以，由惯性矩的组合公式可计算得到

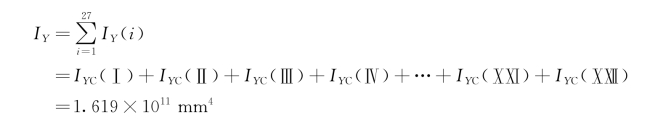
1）下箱梁截面工况下弯矩计算

当抛石管保持架处于工作状态下，根据抛石管保持架静定梁受力分析图4-75与抛石管保持架弯矩图4-77，可得下箱梁截面受到的绝对值最大弯矩时最大弯矩为63.61 k N·m。

2）下箱梁截面工况下正应力计算

通过查找资料可知，横截面任意一点的正应力计算如下：

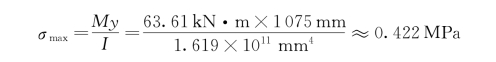
此时其所受正应力远远小于Q345D钢材的许用正应力。