只有当定、转子极对数相等时才能产生平均电磁转矩。对于绕组式感应电动机在改变定子绕组接法并改变极数时，必须同时改变转子绕组的接法以保持定、转子极数相等，这使得变极接线控制显得复杂。而笼型感应电动机当定子极数变化时，其转子技术能自动跟随保持相等。所以，变极调速一般用于鼠笼型感应电动机。

3.2.3.1　变极调速的原理

变极调速的基本原理是：在定子频率一定时，改变定子的极对数即可改变同步转速，从而达到调速的目的。

如图3.13所示，电动机的定子每项绕组都由两个完全对称的“半相绕组”所组成。以A相为例，它是由“半相绕组”a1x1和“半相绕组”a2x2组成的。

当两个“半相绕组”串联时，如图3.13（a）所示，形成的是一个2p=4极磁场，如图3.13（b）所示，如果将这两个“半相绕组”并联，如图3.13（c）所示，所形成的是一个2p=2极磁场，如图3.13（d）所示。

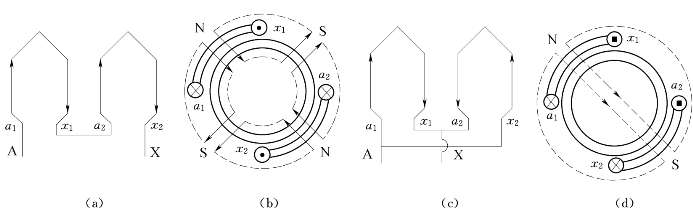
图3.13　三相异步交流电动机变极时半相绕组的接法

比较图3.13（b）和（d）可知单绕组倍极比的变极原理：只要将两个“半相绕组”顺串，即两个“半相绕组”中的任何一个“半相绕组”的电流反向，极对数就增加了一倍。当将两个“半相绕组”反并时，极对数就减少了一半。

为达到非倍极比的变极目的，如4/6极等，也可以用改变绕组接法；如果所需的变极技术相差很大，如6/24极，这时如用一套绕组来实现变极比较困难，因此可以在定子上安装两套绕组，一套绕组是2p=6而另一套为2p=24极。使用时根据速度要求选中一套绕组而让另一套开路；如果定子上有两套绕组，而且每套绕组又都可以变极，那么就可以实现更多的变极方案。

3.2.3.2　两种常用的变极调速方案

1.变极的原理接线

如图3.14（a）、（c）所示的两种接法，每相的两个“半相绕组”是顺串的，因而是倍极数，设为2p=4极。当图3.14（a）所示的接法改为图3.14（b）所示的接法（称为Y→双Y变极）或将图3.14（c）所示的接法改为图3.14（d）所示的接法（称为△→双Y变极）时，都使每相的两个“半相绕组”变成反并联，极数减半，变成2p=2极。反之亦然。显然，这两种变极方案的三相绕组只需6个引出端点，所以接线最简单，控制最方便。

变极接线时必须要注意：首先，变极时，如图3.14所示，为了使变极前后三相基波磁动势在空间仍然互差120°，保持对称；A、C相绕组是a1x1和c1z1中的电流反向而B相绕组是b2y2中电流反向。其次，为了保证变极前后电动机的转向不变，变极时必须同时改变外施电源的相序。假设p=1时A相绕组轴线A的位置为0°，B为120°，C为240°，设此时旋转磁场沿逆时针方向旋转。在p=2时，A仍为0°，而B为120°×2=480°（相当于120°）。如果外施电源相序不变的话，则变极后旋转磁场将沿顺时针方向旋转，使电动机反转。

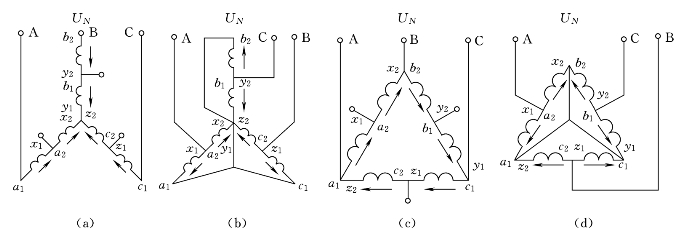
图3.14　三相异步交流电动机的两种常用的变极方案

2.变极调速的机械特性

三相感应电动机的最大转矩Tm、临界转差率Sm及其转矩TQ分别为(www.daowen.com)

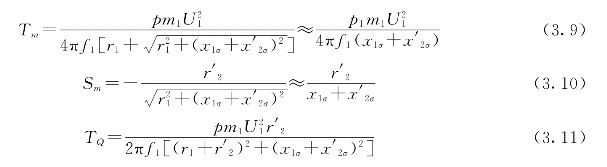
对于Y⇌双Y变极方案，变极前后相电压不变。极对数，即同步转速n1⇌n＇1=2n1；假设变极前后的两个“半相绕组”的定、转子漏阻抗不变，则有。将这些关系代入上式可得：。由此可以定性地画出Y⇌双Y变极的机械特性。如图3.15所示。

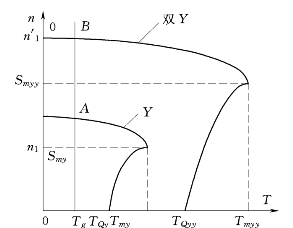
图3.15　Y⇌双Y变极调速的机械特性

对于△⇌双Y变极方案，变极前后相电压U1=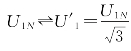；极对数为（使n1⇌n＇1=。将这些关系式代入上述的三个式子可得：SmΔ=Smyy，TmΔ。由此可以定性地画出△⇌双Y变极调速时的机械特性。如图3.16所示。

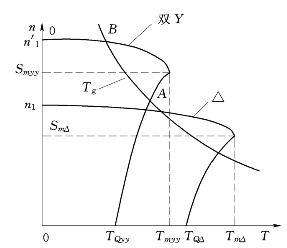
图3.16　Y⇌双Y变极调速机械特性

3.变极调速时的允许输出

感应电动机调速时的允许输出也是指在整个调速过程中，在保持定、转子绕组每个线圈中电流为额定值的条件下，该机所允许输出的功率与转矩的限制值。为了简化起见，假设变极前后的效率与功率因素不变，即η=η＇且cosφ1=cosφ＇1，变极前后的输出功率或转矩的关系分别为

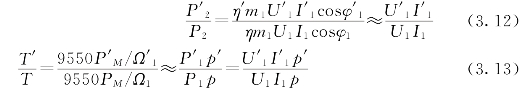
对Y⇌双Y变极方案，由于而定子所允许的相电流为I1=I1N，I＇1=2I1N，则由上式可得

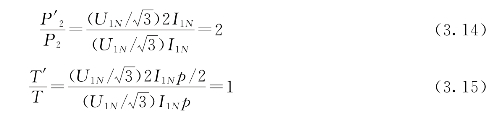
由此可知，对于Y⇌双Y变极调速，如果保持变极前后电源电压即每个线圈中电流不变，则其输出转矩不变，所以是一种较适合于恒转矩负载调速方式，但是这时必须注意变极前后过载能力的变化。

对于△⇌双Y变极方案，由于而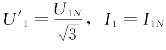而I＇1=2I1N，则

由此可知，对于△⇌双Y变极调速，如果保持变极前后电源电压及每个线圈中的电流不变，则其输出功率基本不变，所以这是一种近似恒功率调速方式。

变极调速简单可靠，成本低，效率高，机械特性硬，既可适用于恒转矩调速也可适用于恒功率调速。但是，它是一种有机调速而且只能是有限的几档速度，因而适用于对调速要求不高且不需要平滑调速的场合。