有静差调速系统是通过放大转速偏差实现调速，没有偏差就没有放大输出，所以系统始终有静差。系统静态误差与放大环节的放大系数有关，放大系数越大，转速的静态误差越小，为了减小静态误差，提高控制的精度，只有增大放大环节的放大系数，但放大系数的增加是有限的，放大系数过大会使系统的动态性能变坏。如果采用具有积分记忆功能的积分（I）或比例积分（PI）调节器代替比例调节器后，可使系统稳定，还有足够的稳定裕度，从而形成了无静差调速系统。

1.积分调节器（I调节器）

积分调节器的电路原理如图1.22所示，假定运算放大器是理想的，则有

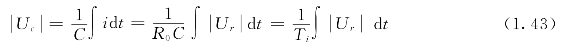
其中

当Ur是阶跃信号时，，若Uc（0）=0，则C=0。可以推出：与t呈线性关系。需要注意的是，输出不会无限增大，由于积分调节器的限幅作用，只能随时间增长至幅值Ucm。

Ur是其他输入信号或Uc的初始条件不为零的情况下的输出也很容易由式（1.43）求得。

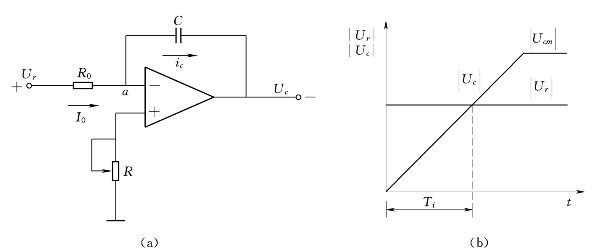
图1.22　积分（I）调节器

（a）积分调节器原理图；（b）积分调节器输入输出关系

如果单闭环调速系统中采用积分调节器，则输出电压Uc是输入电压ΔU的积分，由式（1.43）可知

由式（1.44）可知，积分器的输出量正比于输入量的积分，Uc与ΔU和横轴包围的面积成正比如图1.23所示，所以积分器具有积累作用；当输入为零时，ΔU和横轴包围的面积等于零，积分器的输出保持不变，具有保持作用；当输入突然发生变化时，输出不会发生突然变化，具有延缓作用。

在动态过程中，由于转速变化而使ΔU时，只要其极性不变，即只要保证Ug>Uf，输出电压Uc便一直增长，至ΔU=0时，Uc才停止上升。不到ΔU变负，Uc不会下降。值得特别注意的是，当ΔU=0时，Uc并不是零，而是一个恒定的数值Uc0，这是积分控制和比例控制的明显区别。正因为这样，积分控制可以使系统在偏差电压为零时保持恒速运行，从而得到无静差调速。在突加负载引起动态速降时产生电压ΔU，达到新的稳态时，电压ΔU又恢复到零，但已从Uc0上升到Uc1，这里的Uc的改变并非仅靠ΔU本身，而是依靠ΔU在一段时间内的积累来实现的，实质是积分调节器的电容元件储能性质的具体实现。无静差调速系统当负载突增时的动态过程曲线如图1.23所示。

2.比例积分调节器（PI调节器）

PI调节器的输出由比例和积分两个部分叠加而成，集合了比例调节器输出动态响应快，积分调节器稳态精度高的双重优点。比例积分调节器电路原理图如图1.24（a）所示。为了避免涉及反相问题，Ur、Uc取绝对值

图1.23　积分调节器的输入和输出动态过程

（a）ΔU为阶跃信号；（b）ΔU为干扰变化函数

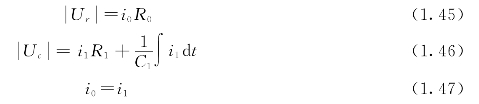
由式（1.45）、式（1.47）得

将式（1.48）代入式（1.46）中得(www.daowen.com)

其中

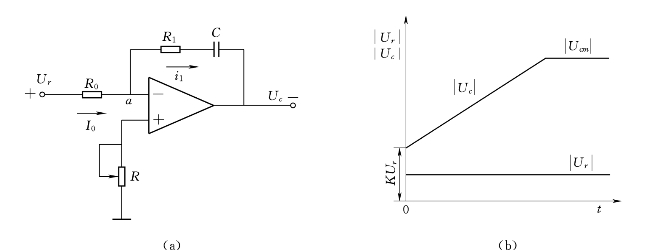
图1.24　比例积分（PI）调节器

（a）比例积分调节器原理图；（b）比例积分调节器输入输出关系

如果单闭环调速系统中采用比例积分调节器，则输出电压Uc与输入电压ΔU的关系式为

由式（1.50）可以看出，比例积分调节器的输出电压Uc由比例部分KΔU与积分部分两部分组成。当输入信号ΔU突然变化时，比例部分KΔU立即起作用，使得输出信号Uc发生突变，然后积分部分起作用，输出信号按积分规律变化。当输入为零时，输出将保持不变。

总之，比例积分控制具备了比例控制和积分控制的优点，又弥补了各自的缺点。比例调节器能快速响应控制作用，而积分调节则消除稳态偏差。

3.由比例积分调节器组成的无静差调速系统

如图1.25所示是由比例积分（PI）调节器构成的单闭环无静差调速系统原理图，若将调节器改为积分调节器，则变成用积分调节器构成的无静差调速系统。

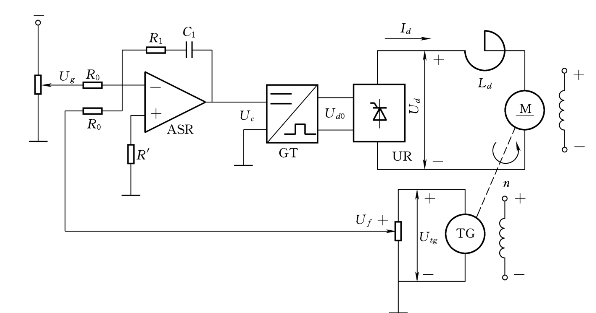
图1.25　由比例积分（PI）调节器组成的无静差调速系统

启动时突加给定电压Ug，由于机械惯性，电动机转速缓慢增加，转速反馈电压Uf很小，比例积分调节器的输入电压ΔU=Ug-Uf较大，输出电压Uc立即达到较大值，使整流电压Ud0瞬时达到较大值，并不断增大，由于此时转速较小，电动机电枢电流迅速产生一个较大的冲击，使电动机转速迅速升高。因此它的启动过程较快，但冲击较大。当稳定运行时Ug=Uf则ΔU=0，Uc保持不变，实现无静差调速。

拖动系统的负载转矩突然增大，电动机转矩来不及跟随负载转矩变化，转速n将下降，Uf随着减小，调节器的输入ΔU>0。调节器输出Uc升高，整流电压Ud0增大，电动机电枢电流Id随着增大，最后达到电动机转矩T与负载转矩TL重新平衡，n回升到原来的数值。动态调节过程如图1.26所示。

如果负载突然减小，转速n将上升，Uf随着升高，调节器的输入ΔU<0，与启动时相反。对于不可逆调速系统而言，由于晶闸管变流器不能流通反向电流，因此只能迫使主电路的电流迅速为零，但不产生电气制动转矩，系统只能依靠负载转矩制动减速。最后达到电动机转矩T与负载转矩TL重新平衡，n降到原来的数值。此时系统可能会产生振荡。可以用可逆调速系统代替不可逆系统来解决这一问题。

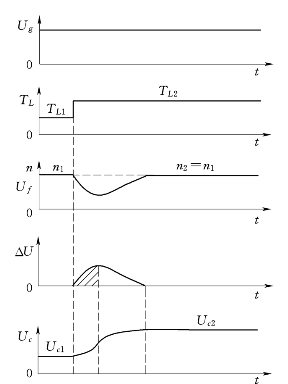
图1.26　无静差调速系统突加负载的动态过程图

当系统要减速制动时，使Ug突然减小（如果停车则使Ug=0），由于系统的机械惯性，转速不可能立即减小，Uf>Ug，ΔU与启动时相反，立即使调节器输出反向电压。对于不可逆调速系统而言，由于晶闸管变流器不能流通反向电流，因此只能迫使主电路的电流迅速为零，但不产生电气制动转矩。此后，系统只能依靠负载转矩制动减速。

“无静差”只存在于理论上，因为积分或比例积分调节器在稳态时电容两端电压不变，相当于开路，运算放大器的放大系数理论上为无穷大，所以才能达到输入电压ΔU=0，而输出电压Uct为任意所需值。实际上，这时的放大系数是运算放大器本身的开环放大系数，其数值虽大，还是有限的，因此仍存在着很小的ΔU，也就是说，仍有很小的静差Δn，只是在一般精度要求下可以忽略不计而已。无静差调速系统结构图如图1.27所示。

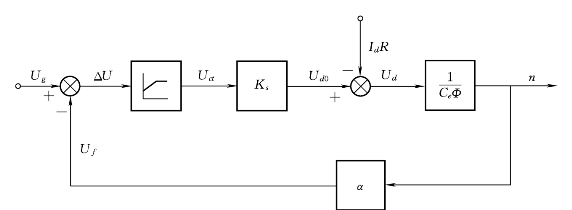
图1.27　由比例积分（PI）调节器组成的无静差调速系统结构图