直流伺服电动机的动态特性是指当给电动机电枢绕组加上阶跃电压时，转子转速随时间变化的规律。这一规律可用表达式ω=f（t）来描述。

直流伺服电动机的动态过渡过程的产生原因是由负载转动惯量引起的机械惯性和电枢电感引起的电磁惯性导致的。

图1.2所示的电枢回路中动态电压平衡方程式为

式中：ia、ea和ua分别为电枢电流Ia、电枢反电动势Ea和电枢绕组两端的控制电压Ua在过渡过程中的瞬时值；La为电枢绕组电感。在过渡过程中，直流伺服电动机的电磁转矩Tm除了要克服负载转矩TL外，还要克服轴上的惯性转矩，因而它的动态转矩平衡方程式为

式中：J为转子轴上的总转动惯量。

将式（1.3）中的Ia换成ia并代入式（1.13），可得

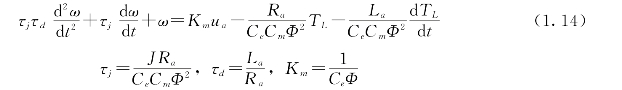
式中：τj、τd、Km分别为机电时间常数、电磁时间常数和静态放大系数。

当直流伺服电动机带有恒定负载时，则，可简化成

在空载条件下，即TL=0时，式（1.15）还可以进一步简化成

(www.daowen.com)

对式（1.16）进行拉氏变换，得出电动机的传递函数

在大多数情况下，τj>4τd，此时τd可以忽略不计，式（1.17）可写成

可见，这时电动机是一个一阶惯性环节。在单位阶跃电压信号输入时，角速度的响应函数为

其变化曲线如图1.8所示，电动机的角速度按指数规律从零逐渐增加到稳态值Km，过渡过程的时间常数τj。

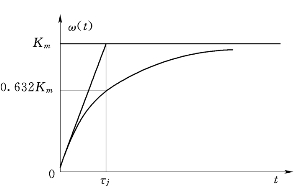
图1.8　直流伺服电动机的单位阶跃响应

根据式（1.6）和式（1.7）得

式中：Td/J为力矩—惯量比。

可见通过加大力矩—惯量比的方法，即可加快过渡过程，又不至于引起振荡，直流伺服电动机就是基于这一原则设计的。