1.数学模型

同时考虑无功投切和变压器分接头调整对系统状态的影响，根据式（9-5），则有：

而由式（9-5）同样可得：

说明网损的变化由两部分构成，一部分是由于参数变化所引起的，而另一部分是由于状态变量的变化而引起的。将式（9-17）代入到式（9-18）中，得到：

地区电网无功电压控制的目的是为了提高电压合格率、降低网损。在实际的应用过程中，都是以网损最小为目标函数，满足电压上下限和变压器、无功等调节设备的容量限制。因此，可以描述为如下的数学模型，目标函数：

min P_Loss=min P_Loss0+min ΔP_Loss （9-20）又假设在本状态之前的电网P_Loss0（x₀，y₀）是确定的，则目标函数可以简化为

满足如下的约束条件：

式中 x_min，x_max——状态变量上下限约束。即：

上式是指节点电压幅值的约束，将式（9-17）代入，得：

以及：

式中 Δw_min，Δw_max，Δy_min，Δy_max——无功补偿装置和变压器分接头调整的容量限制，求取方法同上。

对于计算过程中雅可比矩阵的逆阵，可以采用三角分解的方式确定。则由式（9-21）、式（9-24）和式（9-25）构成了无功电压实时控制的数学模型，因为数学模型是线性的，提高了分析问题的复杂程度和效率。

2.计算方法

在无功电压控制过程中，等式约束主要体现在无功功率平衡上。对地区电网来说，电容器组投切后无功功率的平衡主要反映在关口点（平衡节点）的无功注入上，电容器组的投切容量大，关口点的注入就少。所以无功平衡主要是电容器组的投切容量和平衡节点的注入无功之间的平衡问题。

在上述优化模型中，平衡节点的无功注入是根据状态变量确定的，因此可以不考虑无功功率平衡的偏差方程，优化结果所体现的平衡节点注入无功功率也是最优的。(www.daowen.com)

因为电容器组的投切与变压器分接头的调整对降损效果差别较大，特别是变压器分接头的调整对降损的效果是不明显的，在实际的计算过程中可以分步来求解，即将整个优化问题分解为两个子问题。

（1）子问题1

对于子问题1，只考虑无功补偿的影响，认为变压器分接头是不调整的，则平衡节点注入功率变化为

约束条件（9-24）变化为

令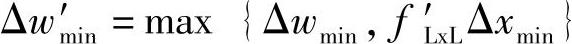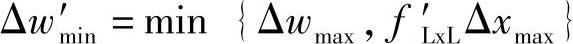，，则子问题1可以表示为

由于上述问题不包括等式约束，所以有：

Δw_L=Δw′_min （9-29）

（2）子问题2

变压器分接头的调整通常是在无功补偿装置调整的基础上进行的，因为电容器组都是整组投切的，由子问题1确定的无功补偿容量取整后也可能造成节点电压越限或者网损增大等现象，可以通过变压器分接头的调整进行进一步优化。子问题2可以描述为如下的形式，平衡节点注入的功率可以表示为

约束条件变化为

以及：

Δy_min≤Δy≤Δy_max （9-32）

上述子问题的计算过程可以简化如下：首先取Δy=Δy_min，判断不等式约束是否满足，如果满足则计算就中止了；否则，按照矩阵f′_Sy-f_S′_xL（f′_LxL）-1f′_Ly中元素为灵敏度对Δy进行修正；上述过程一直持续到满足约束式（9-31）为止。

子问题1和子问题2的计算可以单独进行，也可以同时进行。在无功电压实时控制过程中，因为电容器组不是频繁调节的，所以子问题1和子问题2的计算周期也不同，子问题2的计算周期短，而子问题1的计算周期较长。甚至是，当节点电压偏差较小时，直接按照式（9-7）计算需要调整的变压器档位就可以了。