从上面的数学模型可以看出，总成本C受到总补偿容量、分组情况、动态补偿容量等几个因素的影响。当总补偿容量上升时，Q_C≥Q_Dt的时段数将会增加，配电站运行成本C_S下降，相应地，因增加容量将使得投资成本C_L整体上升；在总补偿容量Q_C不变的前提下，分组组数M的增加可使小组组合级差ΔQ或最大单组的容量Q_M下降，从而集中控制占总补偿容量的比重下降，分散补偿占总补偿容量的比重上升，动态补偿的投资成本C_L2下降，相应地，因增加分组亦将导致与分组数相关的投资成本上升；与此相反地，在总补偿容量Q_C不变的前提下，分组组数M的减少可使小组组合级差ΔQ或最大单组的容量Q_M上升，从而集中控制占总补偿容量的比重上升，分散补偿占总补偿容量的比重下降，相应地因减少分组亦将导致与分组数相关的投资成本下降，运行成本C_S上升。

下面进一步将数学模型（8-50）化简，将Q_C2表示为

Q_C2=Q_C-Q_C1 （8-60）

并利用式（8-52），用m₁和Q_M来替换Q_C1，从而有：

Q_C2=Q_C-（m₁+1）Q_M （8-61）

将式（8-61）、式（8-53）带入式（8-58），有：

将式（8-61）、式（8-53）带入式（8-59），有：

将式（8-51）、式（8-60）、式（8-61）、式（8-62）、式（8-63）带入式（8-50），从而数学模型化简为

此时，模型中只含有m₁、m₂、Q_C和Q_M四个变量，且彼此存在制约的关系，不妨单独对Q_M分析：当固定m₁、m₂、Q_C时，上式等号右边第1项与第4项均为定值；而第2项中由于单位容量的动态补偿成本c₁必然高于电容器成本b₁，故第2项为负值，且随Q_M上升而单调递减；第3项中由于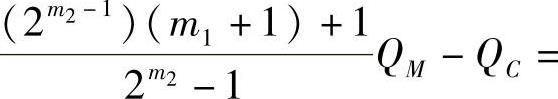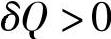，故第3项为正值，且随Q_M上升而单调递增。

考虑电容器均装设在配电站（配变）的低压侧，并认为国产10kV、0.4kV电容器组均有标准化生产规格，从而电容器大组容量Q_M只能取以下标准容量：

Q_M =100，300，600，1200，1800，2400，3000kvar （8-65）

在此基础上对电容器大组组数m₁、小组组数m₂进行约束，考虑大组组数不宜过多，取5组为上限；小组组数亦不宜过多，取5组为上限，且至少应有2组：

m₁ =0，1，2，3，4，5 （8-66）(www.daowen.com)

m₂ =2，3，4，5 （8-67）

从而约束条件式（8-51）～式（8-57）简化为

该数学模型是混合整数非线性规划问题，且目标函数的控制变量之间存在较强关联无法解耦计算，故应根据式（8-28）求出总补偿容量的取值范围Q_C，min≤Q_C≤Q_D，max，并对其进行离散化处理，此时数学模型简化为离散变量的非线性规划问题，可选用适于处理该类问题的人工智能类算法进行求解。

需要说明的一点是：式（8-68）与式（8-69）可能没有交集，此时分两种情况讨论：

1）式（8-68）中Q_M的下限大于式（8-69）中Q_M的最大容量规格，此时有：

该下限值是由：

推导得出的，该不等式的破坏意味着动态补偿容量Q_C2小于组合级差ΔQ时没有可行解，此时应考虑放宽该约束，认为动态补偿容量Q_C2不小于组合级差ΔQ且小于最大单组容量Q_M，否则电容器小组可用一个大组容量Q_M来代替，小组就失去存在的意义了。从而，当Q_C≥Q_D，t时，通过电容器组与动态补偿装置的配合可以将无功负荷完全补偿，故应对目标函数式（8-64）中等号右边第3项进行修改，修改后的目标函数为

2）式（8-68）中Q_M的上限小于式（8-69）中Q_M的最小容量规格，此时有：

该上限值的三个约束量中，第一项是《原则》中对各电压等级变电站装设的并联补偿电容器单组容量的限制；第二项是本文采用的单组电容器投切引起母线电压波动的限制；第三项是由式（m₁+1）Q_M=Q_C1≤Q_C得出的。三个约束量中第二项2.5%S_SC由于没有明确规定因而可以放宽，为了将Q_M的上限增大，可去掉第二项，从而约束条件式（8-68）变为

若Q_M新的上限仍小于最小容量规格，则说明在当前大组组数m₁已定的情况下总补偿容量Q_C过小，原因既可能是当前大组组数m₁取值不合理，也可能是该配电站的负荷较轻，亦或两者皆有。此时可直接给目标函数赋一个较大值，令该可行解在人工智能算法寻优过程中被屏蔽掉。

若在不同的[Q_C，m₁，m₂]取值下Q_M所有可能的上限值均小于最小容量规格，则说明该配电站负荷太轻，在典型日负荷曲线的最大负荷时，将母线功率因数从0.90提高到0.95所需补偿的无功功率不足国产电容器规格的最小容量。此时可只装设1组最小规格的电容器并根据负荷情况进行投切，相应地目标函数亦需要进行简化。

同理，当动态补偿装置容量Q_C2小于某个给定下限值时，可认为装设动态补偿是不经济的，此时只需装设电容器组补偿，相应地目标函数亦需要进行简化。至此，10kV配变无功优化配置的数学模型与求解讨论完毕，在完成该电压层面无功优化配置的基础上，对110～35kV配电站应采用相似的方法进行优化配置，并考虑事故状态下的无功备用，完善配电网全网无功的优化配置。