动态规划法是美国学者贝尔曼（Bellman）在20世纪50年代提出的一种动态最优化方法。它的基本原理是，一个多级决策的最优策略具有这样的性质，即无论其初始状态和初始决策如何，从这一决策后所导致的新状态开始，以后的一系列决策必须是最优的。这就是构成动态规划模型的条件之一：状态变量必须满足“无后效性”，即如果其状态给定，则在这段以后过程的发展不受前面各状态的影响，亦即过程的过去历史只能通过当前的状态去影响它未来的发展，当前的状态就是未来过程的初始状态。

1.递推公式

动态规划法根据系统的状态按时间或空间分为若干阶段，用数学方法来推算每个阶段的状态而做出决策，从而有效地获得最好的收益。对于电容器组优化投切问题，是以网损最小为目标，满足负荷平衡约束以及电容器组的投切次数等限制。动态规划法的递推公式是

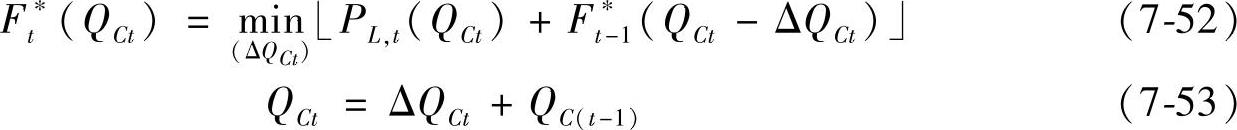
式中 t——阶段号（1，2，…，T）；

Q_Ct =[Q_Ct，i]^T——各个节点的无功补偿向量，假设每个节点都存在无功补偿，对于不存在的节点Q_Ct，i=0，因此维数也为N；

ΔQ_Ct=[ΔQ_Ct，i]^T——在第t时段电容器组的容量变化，电容器组由切到投，则ΔQ_Ct，i=Q_Ct，i，如果电容器组由投到切，则ΔQ_Ct，i=-Q_Ct，i，如果电容器组状态不变，则ΔQ_Ct，i=0；

F^*_{t -1}（Q_Ct-ΔQ_Ct）、F^*_t（Q_Ct）——前t^-1阶段、t的最小网损，在此称为最小状态成本，即F_t表示t时段的状态成本。

根据最优性原理，式（7-52）表示对于前面决策所形成的当前状态（Q_Ct）而言，余下的策略构成最优策略，因为前面的决策（P^*_L，t-1（Q_Ct-ΔQ_Ct）也是最优策略，所以整个决策过程构成最优策略。式（7-53）为状态转移方程，说明相邻两个时段的无功负荷的差正好是需要进行无功补偿的容量。

在动态无功优化问题中的决策变量同样是无功补偿装置的容量，动态规划法就是寻找最佳的电容器组投切组合，在满足无功负荷平衡的条件下，最小化网损，也就是说，将电容器组的容量看成固定的，而对电容器组的投切进行决策。如果电容器组i投，那么Q_Ct，i就是其最大容量；如果电容器组切，Q_Ct，i=0。所以不等式约束是自然满足的。

图7-1为一个4阶段（T=4）和4状态（2组电容器，N_C=2）的动态规划法示意图。方框中的0，1分别表示电容器组的状态，0表示切；1表示投。其中没有考虑（00）组合的状态，这说明两组电容器都没有动作。

2.电容器组投切的转移费用

如前一部分所述，电容器组的投切是有成本的。电容器组的投切次数限制可以用投切成本来表示，即将电容器组的投切成本以转移费用来代替。

图7-1 动态规划法示意图

如前一部分所示，投和切电容器组，其成本是不同的，假设以表示第t时段电容器组投的成本，而以表示第t时段电容器组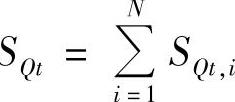切的成本，其中S_Ht，i和S_Qt，i分别表示第i电容器组的投切成本。则递推方程变化为

其中：

式中 ω——分时电价；

ΔT——每个时段的时间长度。

也就是说，状态成本不仅包括网损成本，还包括电容器组的投切成本。

将电容器组的投切成本表示成转移费用之后，可以不考虑投切次数方面的限制。此外，动态优化模型的目标函数发生了变化，不仅增加了转移费用项，而且目标函数的量纲以成本来表示，而不是网损最小化。如图7-1所示，不同时段的状态之间的转移路径增加了权重，此权重即电容器组的投切成本。

3.状态空间简化(www.daowen.com)

动态规划方法的主要缺点是：当时段数和每时段的状态数较多时，出现“维数灾”问题。因此，在动态规划方法的实际应用中，尽量地减少状态数量，是避免“维数灾”问题的关键。对状态进行简化要通过减少时段数和减少状态数量两个方面来进行。

（1）减少时段数量

负荷在一天当中有高峰和低谷，由于不能频繁地进行投切，电容器组一般来说是在高峰时投入，在低谷时切除。因此，在进行动态规划决策时，可以按照负荷曲线的形状确定时段数量，决策的时段只能定在负荷的高峰和低谷期，如图7-2所示。因为要通过调整无功功率在配电网中的流动达到降低有功损耗的目标，所以应以无功变化曲线为基准进行分段。一般情况下，有功和无功的变化趋势基本一致，所以有功无功可以兼顾，分段并不困难。

图7-2 时段的确定示意图

其中，纵坐标代表电容器组的容量和无功负荷，横坐标代表时间，根据负荷峰谷划分电容器投切的时段数是按照电容器组的补偿容量和组数来确定的。如图7-2所示，电容器分为3组，那么可以按照电容器组的容量对负荷曲线进行划分，相应的分成5个时段。

在实际的应用过程中，电容器的分组往往只有2组，所以时段数量也不是很多，与传统的按照一个小时、甚至是半个小时划分时段的做法相比，明显地降低了时段的数量。此外，上述负荷曲线是针对一个节点的，对于整个电网来说，也可以按照上述曲线进行时段划分，只是需要考虑不同节点之间负荷曲线的差异程度。

（2）减少状态数量

如图7-3所示，在一个时段上，状态数量的多少取决于电容器组合方案的多少。在实际的地区电网中，电容器组的分布非常分散，所以可以有非常多的组合方案，势必会造成“维数灾”问题。

但是，地区电网往往是闭环建设、开环运行，相互之间的联络很少，如图7-3所示。不同变电站无功的支持只是纵向的，而很少有横向的，所以可以按照地区电网的这种特点进行分区决策。在220kV母线下，左边的110kV变电站和35kV变电站构成一个区域；而右边的一个110kV变电站为一个区域。那么，可以分区确定电容器组的投切决策，这样可以大大地降低电容器组的组合数量，即降低了状态的数量。但是，有多少个分区就需要进行多少个动态规划决策。

此外，考虑节点电压限制的不等式约束也能对状态变量空间进行简化。对于每种状态进行计算，判断节点电压是否越限。如果越限，则说明此状态是不可行的，应该剔除；否则，是可行状态。因为只是考虑电容器组动作对节点电压的影响，节点电压的限制可以适当放宽一些，而通过调整有载调压变压器分接头进行调整。

图7-3 典型地区电网结构图

4.计算流程

采取状态变量空间简化以后，动态规划法的计算流程如下：

1）令t=0，首先设定各个电容器组的初始状态，以及初始状态成本F_t=0；

2）从第1个阶段开始，令t=1；

3）根据负荷水平进行潮流计算，计算各个不同电容器组合Q_Ct（状态）下的网损P_L，t以及节点电压；并检查节点电压约束式是否满足，如果不满足，去掉相应的状态；否则，向下进行；

4）根据ΔQ_Ct=Q_Ct-Q_C（t-1），与t^-1时段相比较，确定电容器组的动作状况，计算各个状态由t-1到t时段的转移费用S_Ht和S_Qt；

5）对于t时段的每个状态，选取t-1时段每个状态成本F_t-1加上相应转移费用成本最小的记做F^*_t-1，并对此路径进行标记，将F^*_t-1与t时段本状态的网损成本进行叠加，作为F_t；

6）判断t=T是否成立，如果是，令F^*_t=minF_t，将标记的最优路径作为最终的电容器投切选择；否则，t=t+1，返回3）。

因为在上述计算过程中每个状态都需要计算潮流，计算量较大，但是经过状态变量空间简化之后，分区进行潮流计算则相对计算量较小。此外，动态规划算法一般也是作为离线计算和分析的工具，计算时间较长也是可以理解的。在实际应用中也可以采用网损估算的方式，这样可以明显的减少计算量。