如前所述，电力系统无功规划主要目的是通过合理配置无功补偿设备的补偿地点、种类和容量，有助于系统在实际运行过程中能够有效地降低有功损耗、保证电压水平，除此以外，还要力争尽量提高系统的电压稳定性。因此，电力系统无功规划是一个多目标、非线性、离散的多目标组合优化问题。

而根据实际规划中侧重点的不同，无功规划的优化目标函数也不尽相同，主要包括：

1）从经济性角度出发的经典模型是将系统的有功损耗最小为目标函数，当系统的传输容量有足够的裕度时，这种只考虑经济效益和基本运行约束条件的做法是适当的。有功损耗最小是最常用的目标函数，也是进行各种电压无功优化控制的基础。

2）从系统安全性的角度出发，采取以系统运行状态（如节点电压幅值）偏离期望值的二次方和最小或者电压稳定裕度最大为目标函数。

3）将经济性和安全性同时考虑，构成同时考虑电压稳定裕度最大和有功网损最小的多目标无功优化模型。即在传统无功规划模型的基础上，引入了静态电压稳定性指标，建立综合考虑系统有功网损最小、电压水平最好和静态电压稳定裕度最大的多目标无功优化目标函数。

1.电压稳定性在无功规划中的体现

2004年，IEEE/CIGRE的联合工作组在“电力系统稳定性的定义和分类”中，依据电力系统物理过程和系统理论、控制理论的一致性要求，按照扰动的大小和关注的时间框架对电压稳定进行了分类和说明。

1）大扰动电压稳定性：指系统经受大扰动后维持电压稳定的能力。这种稳定性是由系统和负荷特性以及连续或断续的控制和保护的相互作用决定的。

2）小扰动电压稳定性：指系统遭受小扰动后维持电压的能力。这种稳定形式受给定时刻的负荷特性、连续或断续的控制影响。可以通过合理假设将系统方程线性化，以便于分析，灵敏度的计算是识别小扰动电压稳定性的有效手段。

在电压稳定的研究初期，电压稳定问题一直被归入静态稳定的范畴，研究集中在用静态的观点、模型和研究方法来探讨电压失稳的机理，主要利用基于潮流方程的研究方法来求取电压稳定的极限运行条件和运行状态，一般不考虑电力系统的非线性。随着对电力系统电压稳定研究的深入，研究人员认识到电压稳定与无功功率的分布情况有着非常紧密的联系。因此，国内外众多学者提出对传统的无功规划方法进行改进，将电压稳定问题引入无功规划，以期在改善无功潮流分布的同时提高系统的静态电压稳定性，即小扰动电压稳定。

在无功规划中计及电压稳定性可以从以下三个方面入手。

（1）补偿地点的选择

在无功规划之初，首先利用电压稳定裕度指标或模态分析法对系统进行电压稳定分析。将系统中的负荷节点按照电压稳定裕度的大小进行排序，并在稳定性较差的薄弱节点安装无功补偿装置，以提高系统的电压稳定性。或者首先对电力系统进行电压/无功分区；然后对负荷分区的所有节点求电压稳定灵敏度，把每个负荷分区电压稳定灵敏度最大的节点作为候选无功补偿节点。这类方法对电压稳定问题的考虑仅局限于补偿点的选取，并不涉及具体的规划计算过程。

（2）将电压稳定裕度指标引入目标函数

理论上应该将电压稳定裕度指标引入无功规划的目标函数中，但是严格意义上讲，求解电压稳定裕度需要利用连续性方法来实现，其计算过程需要反复迭代，比较复杂。因此一般将静态电压稳定性分析指标引入目标函数中，此类指标计算较为简单，便于无功规划过程中的编程实现，但指标计算结果过于保守，在大扰动和电压不稳定状态下会产生一定的偏差。文献[6]将潮流方程雅可比矩阵最小奇异值的最大化引入了无功规划的目标函数。文献[7]引入了电力市场的理论，将无功功率发电费用最小作为最终的目标函数。

（3）将电压稳定问题体现在约束条件中

即将电压稳定裕度大于某一设定值作为无功规划的不等式约束之一，并且要求系统在N-1情况下也能满足电压稳定的不等式约束。上述方法中，对于电压稳定指标的计算如果比较复杂，无疑将增加整个无功规划的计算时间，这为求解大型电力系统的无功规划问题造成一定的困难。

还可以将电压稳定问题同时引入无功补偿点的选取和无功规划的目标函数中。首先，依次计算各个负荷节点的电压稳定裕度指标并按照大小排序。选择裕度指标大于某一预定值的负荷节点作为无功补偿点，并将待规划节点的指标最小作为无功规划的目标函数之一，或者将电压稳定裕度限定在某一范围内作为无功规划的不等式约束，以使规划结果能够有效提高系统的电压稳定性。

2.多目标优化算法

对于多目标的无功规划，势必要采用多目标优化算法予以求解。从20世纪50年代多目标优化问题提出至今，已有大量的专著集中于多目标优化问题的求解方法研究。总地来说，它可分为两大类：一种是采用经典的优化方法，如加权法、目标规划法等；而另一种则是基于进化计算的方法。进化计算是一种模拟生物界进化或活动行为的智能算法，由于其对求解问题的约束条件低，求解质量高，一直被广泛应用于复杂优化问题求解。自从Schaff首次将遗传算法应用于MOP求解以来，应用进化计算研究多目标优化问题，即多目标进化算法研究，一直是优化领域的热点问题。

（1）多目标优化问题的一般描述

与单目标优化问题一样，多目标优化问题包括目标函数、决策变量和约束条件，其一般结构如下：

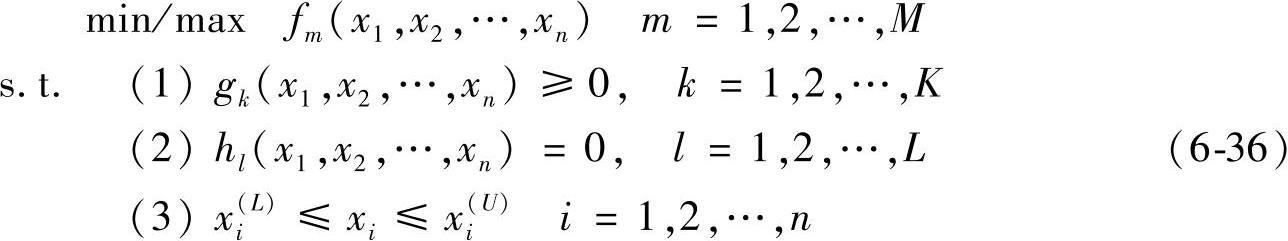
其中，X⊂Rⁿ为决策空间，x=（x₁，x₂，…，x_n）∈X，x^（L）_i和x^（U）_i分别为变量x_i的上下界。

进一步，定义集合Ω=｛x｜g_k（x₁，x₂，…，x_n），h_l（x₁，x₂，…，x_n），x_i（L）≤x_i≤x_i（U）｝为问题（6-36）的可行域，显然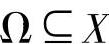。公式（6-36）中的“min/max”表明，每个目标函数可以最小化亦或最大化。

（2）Pareto优化的相关定义

在多目标优化问题中，Pareto优化解是最常用的优化概念。它最早由FrancisYsidro Edgeworth在1881年提出，而后经Vilfredo Pareto推广，其定义如下：

定义1（Pareto支配）：设f：R^N→R^M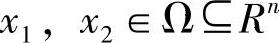，。称个体x₁支配个体x₂，当且仅当f（x₁）部分地优于f（x₂），即∀m∈｛1，…，M｝，f_m（x₁）≤f_m（x₂）∧∃m∈｛1，…，M｝，f_m（x₁）＜f_m（x₂），记做x₁≤x₂。如果对于所有的m∈｛1，…，M｝，都有f_m（x₁）＜f_m（x₂），则称个体x₁强Pareto支配个体x₂，记做x₁＜x₂。

定义2（Pareto最优解）：个体x^∗∈Ω称之为可行解集合Ω中的Pareto最优解，当且仅当集合｛x｜x≤x^∗，x∈Ω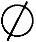｝=。同理，个体x^∗∈Ω称之为可行解集合Ω中的弱Pareto最优解，当且仅当集合｛x｜x＜x^∗，x∈Ω｝=。

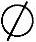定义3（Pareto最优解集）：给定可行解域Ω，则问题的Pareto最优解集X^∗为Pareto最优解的集合，定义为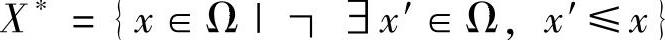：。另外，Pareto最优解集在目标函数空间上对应的集合称之为Pareto前沿面，记为PF∗。

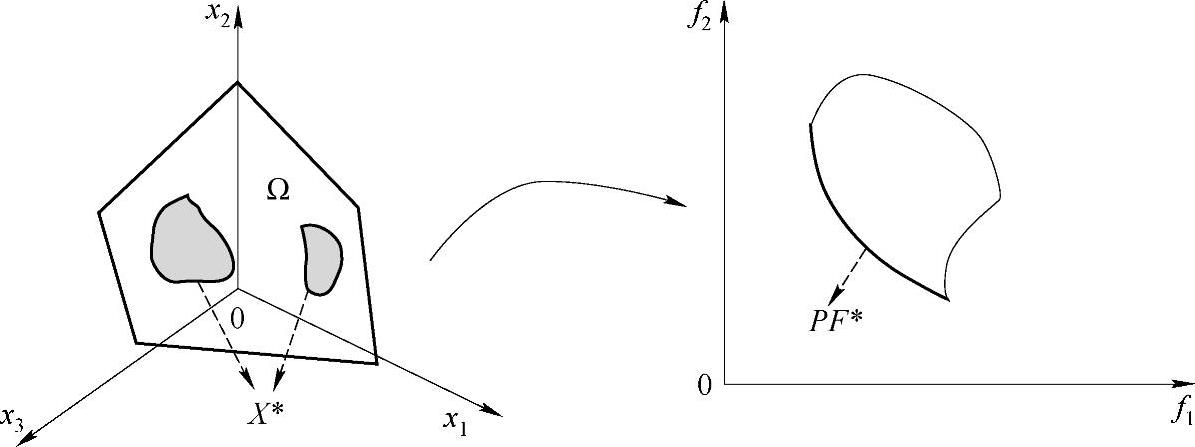
图6-7 Pareto最优解集和Pareto前沿面示意图

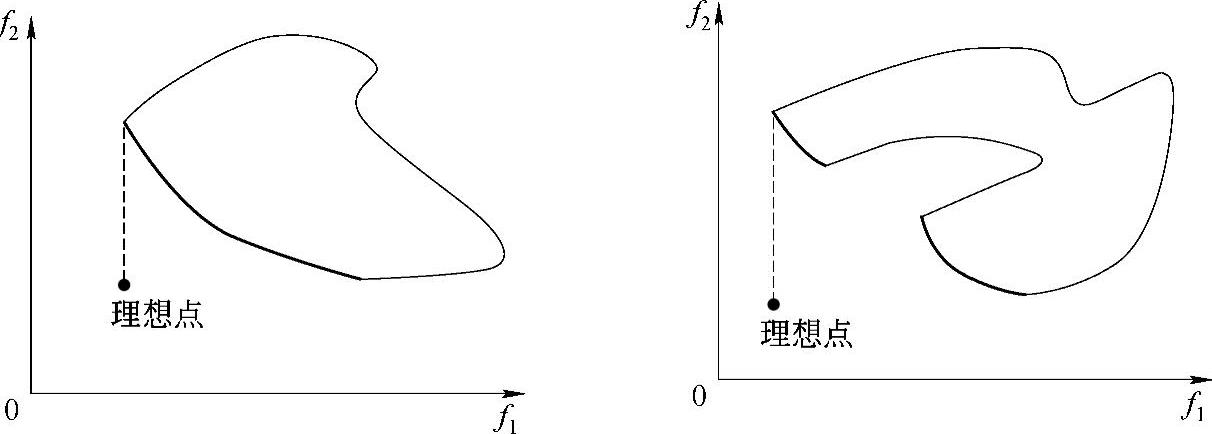
图6-8 理想点示意图

定义4：理想点（ideal point）：给定目标向量Z^∗=f（x），Z^∗∈R^M，称Z∗为理想点当且仅当它的每一个分量z^∗_i（i=1，2，…，M）为对应目标函数的最优解的目标函数值，即

定义5：被支配域（Dominated Area）：对于个体x∈Ω，其被支配域定义为集合｛x′∈Ω｜x≤x′｝。

定义6：支配域（Dominating Area）：对于个体x∈Ω，其支配域定义为集合｛x′∈Ω｜x′≤x｝。

（3）经典的多目标优化算法

在多目标优化问题中，生成Pareto最优解集是求解的重要一步，但是，决策者所需要的仅仅是其中的某一个解。因此，需要结合决策者的偏好信息，得到Pareto最优解集的全序，从而选择决策者最满意的解。根据决策者偏好参与求解过程的方式，可将传统的多目标优化算法分为如下几类：

1）无偏好方法（non-preference methods），指求解中没有利用明显的偏好信息；

2）后偏好方法（posterior methods），指搜索完成之后再做决策；

3）前偏好方法（priori methods），指决策之后再进行搜索；(www.daowen.com)

4）交互式方法（interactive methods），指在搜索过程和决策过程交互进行。

① 无偏好方法

在无偏好方法中，不考虑决策者的偏好，所有的目标都被视为同等重要。故其主要应用于决策者对问题的求解无特别要求的情形。全局指标方法（method of the global criterion）又称为折衷规划方法（compromise pro-gramming），是一类广泛应用的无偏好方法。在选择参考点和距离度量指标后，其通过最小化参考点与可行解的距离来生成Pareto最优解。问题构建如下：

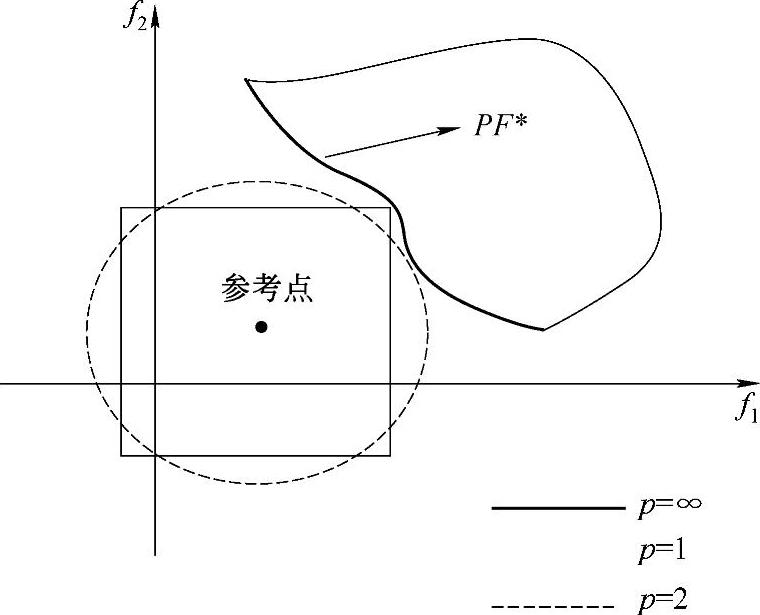
图6-9 全局指标方法中不同p值示意图

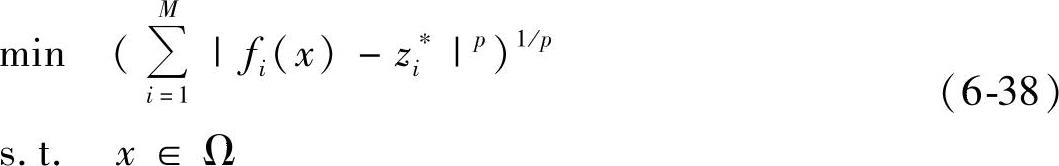
其中z^∗_i表示参考点，不同的p值表示不同的距离范数。参考点的选择在此方法中格外重要，因为公式（6-38）生成的解不会优于预先设置的参考点。一般来说，可以选择理想点作为问题的参考点。另外，选择不同的p值也会得到不同的解，p值经常设定为1，2或者∞。

② 后偏好方法

后偏好方法又称为Pareto最优解生成法（methods for generating Paretooptimal so-lutions）。在生成Pareto最优解集（或子集）后，再交由决策者选择最合适的个体。常见的代表方法有权重法（weights methods）、ε-限制法（ε-constraint methods）和可达标量函数法（achievement scalarizing function approach）。其中，基于进化算法的多目标优化方法亦属于后偏好方法。这里简要介绍前一种方法。权重法是一种常见的多目标优化问题的求解方法。它通过对每一个目标赋予一定的权值，将多目标问题转化为单目标问题求解。具体公式如下：

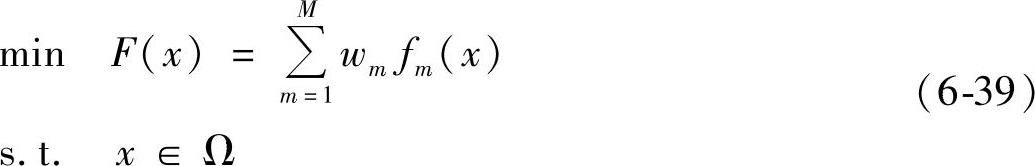
其中w_m≥0，m=1，…，M，且∑w_m=1。通过变化权重值，可以生成不同的Pareto最优解。然而，均匀分布的权重值集合并不一定对应着均匀分布的Pareto最优解集。虽然权重法形式简单直观，但如果目标函数具有非凸的特性，则权重法无法找到Pareto最优解。如图6-10所示，实线部分为非凸的Pareto前沿面。当权值向量取w₁或w₂时，可得到Pareto最优点P点Q。当权值向量为w₃时，虽然其在前沿面有切点R，但其亦在S点与前沿面相交。故权值曲线w₃应继续向左下角移动。可见，当目标函数具有非凸性质的时候，类似图6-10中加粗的Pareto前沿面上的个体在权重法下就无法求得。另外，也有学者将权重法用于前偏好方法中。这时，由于不同的目标有时候代表不同的含义，具有不同的量纲，在赋予权重值之前需要将各个目标正规化，以使它们具有相同的数量级。

③ 前偏好方法

前偏好方法在求解之前，需要了解决策者的偏好信息。其中，常用的方法有价值函数方法（value function method）、字典序方法（lexicographic orderingmethod）和目标规划法（goal programming）。这里简单介绍一下字典序方法。字典序方法操作简单，在实际中应用也比较广泛。首先，需要决策者对所求问题的目标函数的重要性按升序排序。重要性最高、排在首位的目标函数在当前的约束条件下率先优化。显然原问题简化为带约束的单目标优化问题，如果此问题的解是惟一的，则这个解即为原问题的Pareto最优解。否则，优化下一个目标函数，同时加入新的约束条件，即确保排在前位的目标函数的最优值不变。

图6-10 权重法示意图

④ 交互式方法

交互式方法是一种将决策者偏好融合入求解过程的方法。其算法的基本流程如下：

a）初始化，计算理想点，呈现给决策者；

b）生成一个初始可行点；

c）征询决策者的偏好信息；

d）由现有的可行解和偏好信息生成新的可行解，如果新解到达了决策者的满意度，则算法结束，否则继续步骤c）。

可见，在交互式的方法中，决策者的偏好信息引导着求解的进程。进一步，在求解过程中，决策者亦可以随时地根据现有的求解情况随时地更改偏好信息。相比前偏好和后偏好方法，决策者不必事先对所处理问题有明确的偏好结构，实际上，决策者可以在交互的求解过程中逐渐学习问题的结构信息。因此可以说，交互式方法生成的解应为决策者最满意的解。当然，交互式方法一个最重要的前提就是决策者必须可能或者有兴趣参与求解过程中，并根据自己的偏好引导求解方向。

这里介绍一种基于参考点交互式优化方法，即参考点方法（reference pointmethod）。算法描述如下：

a）设循环参数h=1，选择可达标量函数（achievement function），并将问题结构信息呈现与决策者（如问题的理想点）；

b）由决策者确定初始的参考点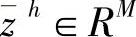，即在每个目标上的期许值；

c）最小化可达标量函数，生成Pareto最优解x^h和相应的z^h；

d）通过变换参考点，生成另外M个不同的Pareto最优解，变化公式如下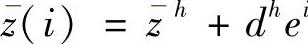：，其中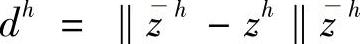，eⁱ表示在第i个目标上的单位向量。

e）如果决策者从M+1个解中选定了一个满意解，则此个体即为最终解，算法结束；否则，决策者另行指定一个参考点，继续步骤c）。

实际上，通过参考点的不同选择，决策者可以逐渐细化Pareto解的位置。如图6-11所示，初始时参考点远离Pareto前沿，决策者得到的Pareto解分布性较广。当决策者进一步选择距离Pareto前沿近的参考点后，最终得到的Pareto解也更加细化，聚集在前沿面的局部区域。

（4）经典多目标优化算法的局限性

虽然经典多目标优化算法在运筹学领域被广泛采用，然而这些数学规划技术还是具有一定的局限性。比如，权重法或基于权重的指标函数法对于Pareto前沿的凸性相当敏感，如果Pareto前沿是非凸的，则最终发现的近似集合不完整，有的方法则对目标函数的可微或者限制条件有诸多要求。另外，在经典的优化方法中，初始点的选择与最终解的获得息息相关。最后，这些方法在一次运行中只能得到一个非支配个体，为了获得Pareto优化解集，需要针对不同的初始点生成不同的非支配个体。因此，在处理实际的复杂问题时，传统的多目标优化算法有其天然的局限性。

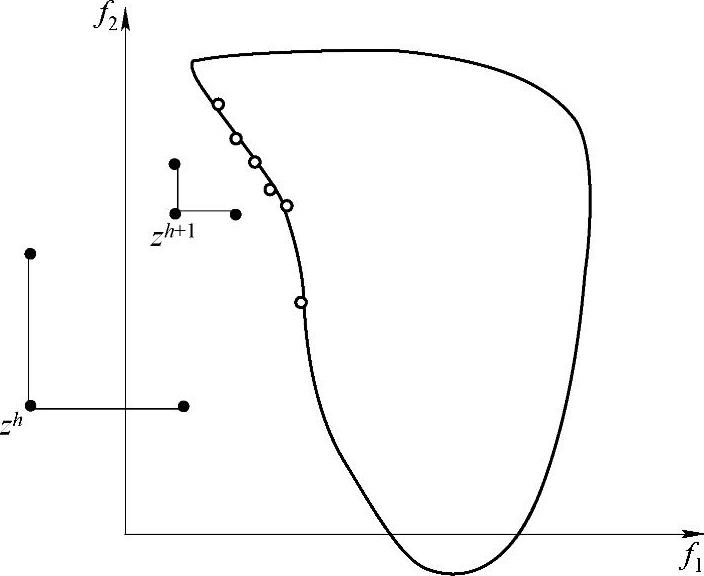
图6-11 参考点变化示意图

（5）基于进化算法的多目标优化方法

将进化计算应用于多目标优化问题的设想最早可以追溯到Rosenberg的博士论文。他在研究中提出了用一组单细胞组织模拟仿真多种性质的设想，但没有付诸实践。而第一个明确提出的多目标进化算法一般认为是Schaffer的向量进化遗传算法，即Vector Evaluation Genetic Algorithm（VEGA），其主要是为了解决机器学习领域的问题。自此以后，诸多学者又提出了形式各样的多目标进化算法，并应用于求解实际问题。

Coello总结了目前的多目标进化算法，并将它们分为两代：第一代强调简洁，第二代强调效率，它们之间的主要区别在于精英个体是否被引入种群的进化过程。第一代MOEAs的雏形始于David Goldberg在1989年出版的有关遗传算法的巨著。在其中，他率先将Pareto优化的概念引入遗传算法的选择过程中，并指明种群的分布性会对算法的收敛性产生至关重要的影响。第一代多目标进化算法一般遵循遗传算法的通用进化模式，采用Pareto排序进行适应值赋值，通过小生境或者适应值共享技术来保持种群分布性。其中，最具代表性的算法有：非支配排序遗传算法（Nondominated Sorting Genetic Algorithm，NSGA），小生境Pareto遗传算法（Niched-Pareto Genetic Algorithm，NPGA）和多目标遗传算法（Multi-objective Genetic Algo-rithm，MOGA）等。

第二代MOEAs的标志就是精英概念的引入。其中，精英个体以两种形式体现：

1）存档种群（Archive Population）又称为外部种群（External Population），即存档种群随进化过程更新并参与生成下一代父代种群；

2）μ+λ的选择模式，即父代种群与子代种群竞争并从中选择优良个体作为下一代父代种群。

无论是何种形式，都亟待解决两个问题：按何种规则生成下一代父代种群和当种群大小超过预设规模如何进行剪枝（truncating）。第二代MOEAs的设计创新主要解决这两个问题。最具代表性的算法有：强度Pareto进化算法（Strength ParetoEvolutioanry Algorithm，SPEA）、强度Pareto进化算法2（SPEA2）、非劣排序遗传算法2（NSGA-II）和Pareto存档进化策略（Pareto Archived Evolutionary Strategy，PAES）等。其中NSGA-II算法作为第二代MOEAs的代表，结构简单，运行效率高，是应用最广、引用率最高的算法。在第二代MOEAs中，除了上述基于遗传算法（Genetic Algorithm）的MOGA，诸多学者还提出了其他的具有群进化特征的智能算法，如基于粒子群算法（Particle Swarm Algorithm）的MOPSO，以及有限加速多目标粒子群算法（SMPSO）；基于模拟退火（Simulated Annealing）的MOSA，如自适应多目标模拟退化算法（AMOSA）；基于蚁群算法的MOACO；基于散点搜索的MOSS，如自适应散点多目标搜索算法（AbYSS）和基于分布估计算法（Estima-tion of distribution algorithm）的MOEDA，如基于规则模型的多目标估计算法（RM-MEDA）。这些算法具有不同的进化机制，但无一例外的都采用的精英个体的概念。这正是第二代MOEAs显著优于第一代的原因。

目前，在多目标无功规划中应用较多的经典算法还是以权重法为代表的前偏好方法。由于无功规划自身问题的复杂性，其可行解空间有可能出现非凸的情况。因此该类方法并不能完全解决所有的问题，而且根据所选权重的不同，最后得出的规划方案也并不是惟一的。

此外，基于进化类算法的多目标无功规划也有很多成果见诸于报道，其中以基于蚁群算法的MOACO、基于粒子群算法（Particle Swarm Algorithm）的MOPSO最为多见。