1.基本思路

以往对城市的电网的无功规划是按照两种思路进行的：

1）按照城市电网规划导则进行，一般为变电容量的10%～30%；

2）按照标准的优化方法进行，与无功优化算法相似。

第一种方法显得较粗糙，而第二种方法太复杂。由于无功功率需要就地平衡，变电站内部的无功补偿主要是为了降低一次侧进线和变压器的无功潮流，进一步降低其中的无功损耗，而不考虑低压侧出线的损耗和变电站之间的无功相互支持。

为了降低一次侧进线和变压器的损耗，并不是无功补偿容量越大越好，还要考虑相应的投资成本。

变电站的接线示意图如图6-4所示。

规划是在负荷预测的基础上展开的，负荷预测通常只是有功负荷预测，也可以做无功负荷预测方面的工作。在一些规程中明确规定了负荷的功率因数，如在导则中规定了35～110kV变电站高压侧的功率因数不低于0.95，则无功负荷可以根据这个功率因数及有功负荷进行确定：

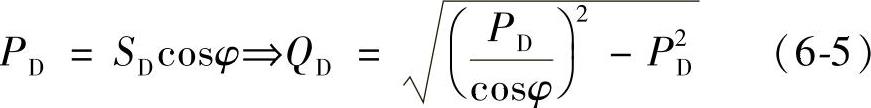
式中 P_D、Q_D、S_D——负荷的有功、无功和视在功率。

2.投资和运行成本

（1）运行成本

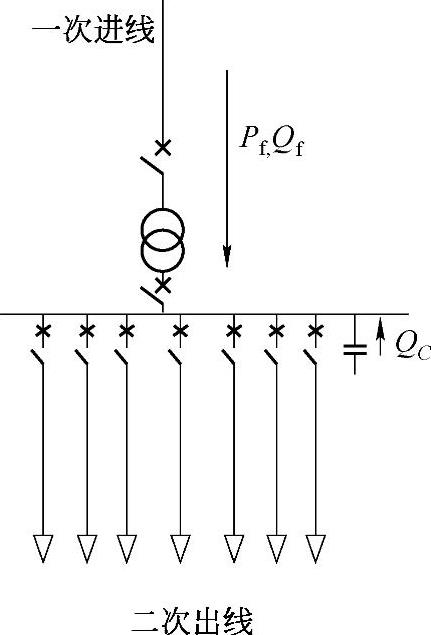
图6-4 变电站的接线示意图

对于变电站出线的网络损耗，因为无功需要就地平衡，所以对于利用无功补偿降低低压侧的线损需要在低压侧考虑。当考虑无功补偿时，高压侧线路的损耗为

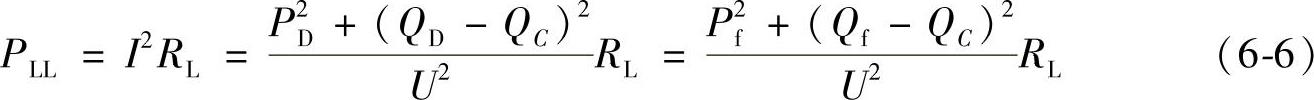
式中 P_D、Q_D——线路末端的负载，可以认为与P_f、Q_f相等；

U——变压器高压侧电压。

变压器的损耗为

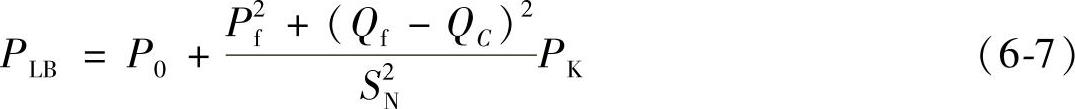
式中 P_K——变压器短路损耗；

P₀——变压器空载损耗；

S_N——变压器额定容量。

总的损耗可以表示为

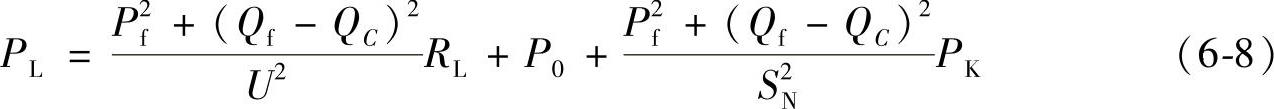
由S_N=I_1NU，I_1N为变压器高压侧额定电流：

整理后得到：

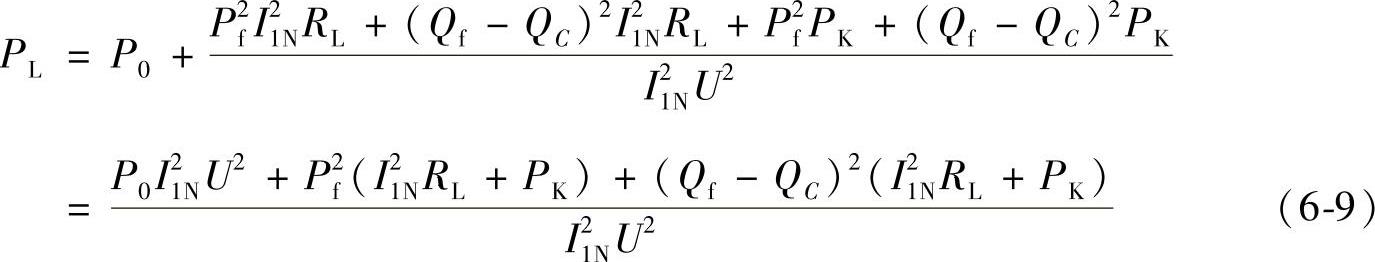
运行成本可以表示为

C_S=ωP_LT （6-10）

式中 ω——电价系数；

T——规划周期。

（2）投资成本

无功补偿装置的投资成本一般可以表示为一个线性函数的形式：

C_L=c₀+B₀Q_C （6-11）

式中 c₀，B₀——常系数。

3.优化模型

（1）目标函数

无功规划问题的目标函数可以描述为

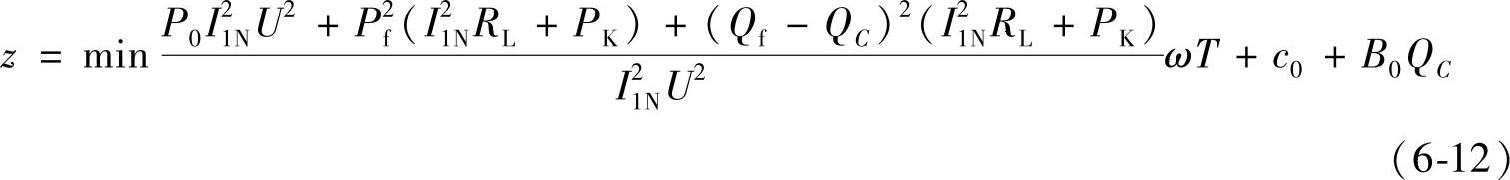(www.daowen.com)

（2）约束条件

对于无功补偿，通常有功率因数方面的限制，可以表示为

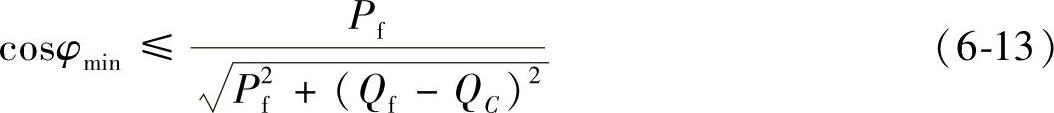
式中 cosφ_min——功率因数的下限。即：

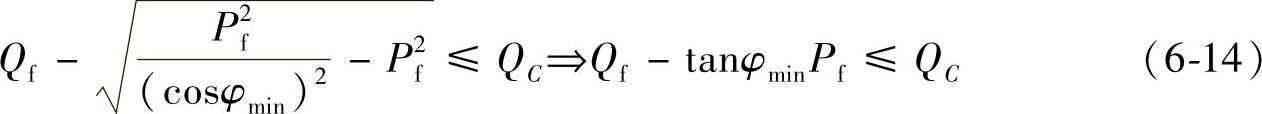
此外，还需要保证线路的电压降落在一定的范围内。假设线路于变压器中的潮流相同，线路的电压降落可以表示为

变压器的电压降落：

当考虑无功补偿后，上述公式变化为

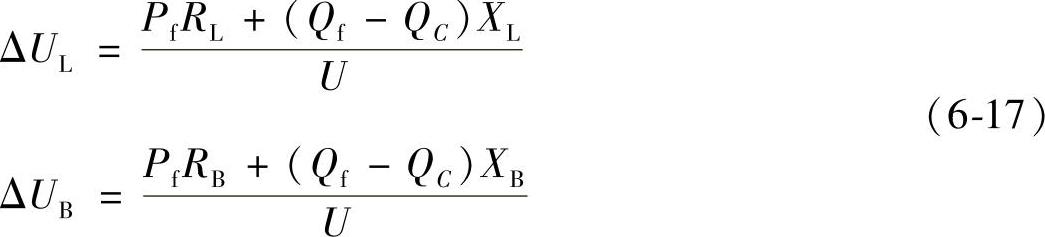
所以有：

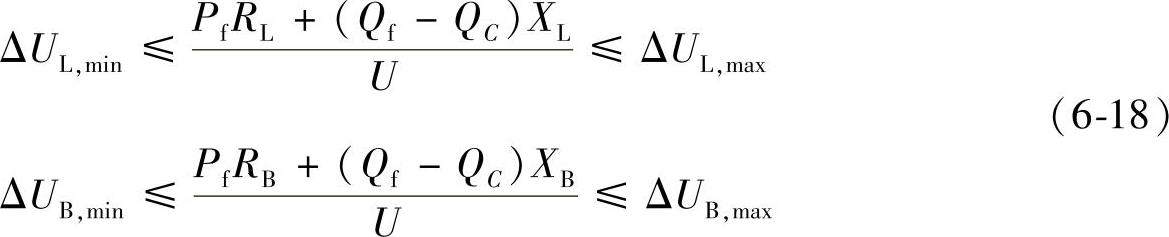
式中 ΔU_L，min，ΔU_L，max，ΔU_B，min，ΔU_B，max——线路和变压器允许的电压降落上下限；

R_B，X_B，R_L，X_L——变压器和线路的电阻和电抗。

将上述公式进行移项和整理，得到：

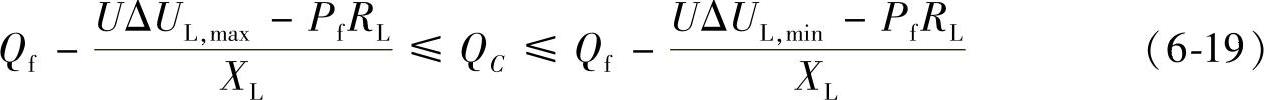
以及：

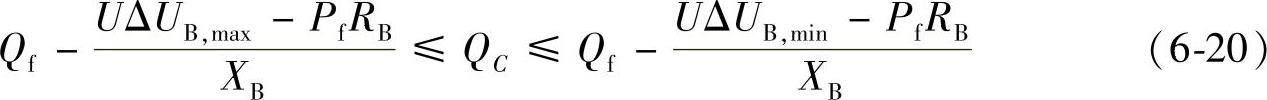
令：

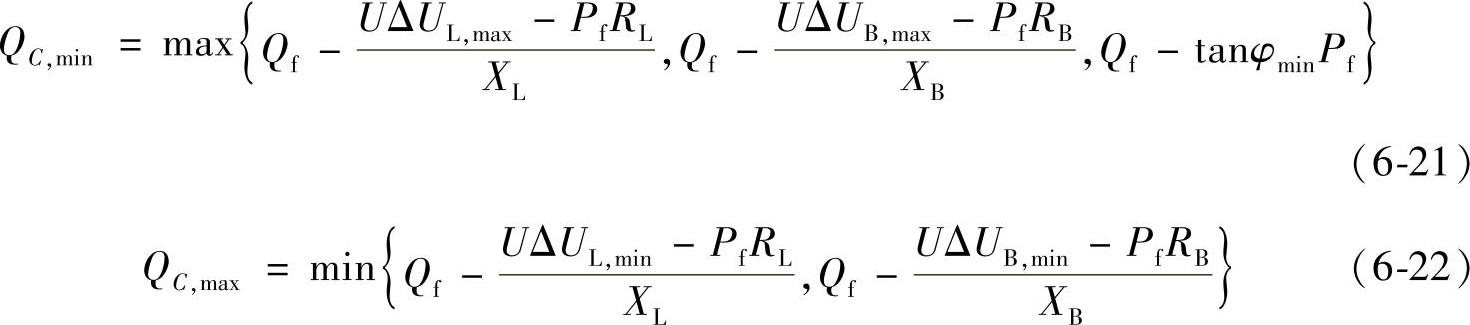
其中：min，max符号表示分别取集合中的最小值或最大值。

无功规划问题满足的统一约束：

Q_C，min≤Q_C≤Q_C，max （6-23）

4.计算思路

上述目标函数是一个二次函数的形式，令：

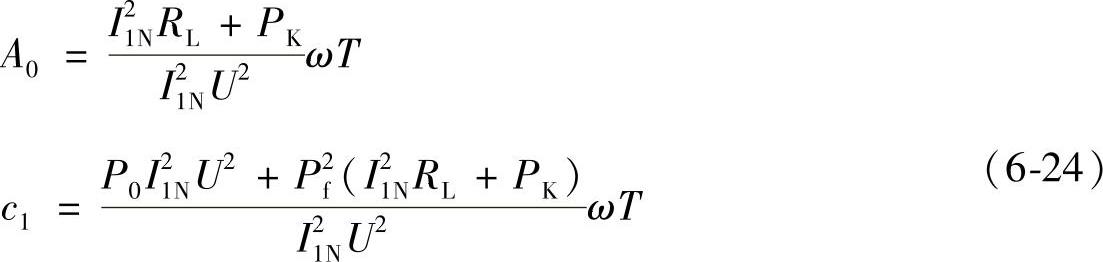
则目标函数变化为

z=min A₀（Q_C-Q_f）²+B₀Q_C+c₀+c₁ （6-25）

令：

C₀=c₀+c₁+B₀Q_f （6-26）

式（6-25）变化为

z=min A₀（Q_C-Q_f）²+B₀（Q_C-Q_f）+C₀ （6-27）

求导后得到：

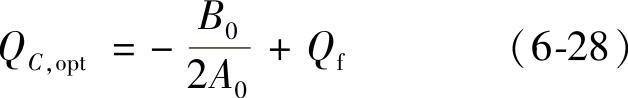
如果Q_C，opt∈｛Q_C，min，Q_C，max｝，则就是最终的解；否则，如果Q_C，opt＜Q_C，min，则最终解为Q_C，min；如果Q_C，opt＞Q_C，max，则最终解为Q_C，max。

如图6-5所示，其中纵坐标为成本，横坐标为无功补偿容量。对于线路和变压器的损耗曲线是二次的，在此曲线的左半部分表示的是运行成本随着无功补偿容量的增加而降低的；而无功补偿装置的投资成本是线性的，是随着无功补偿装置容量的增加而上升的。两种曲线的交点就是最优解。

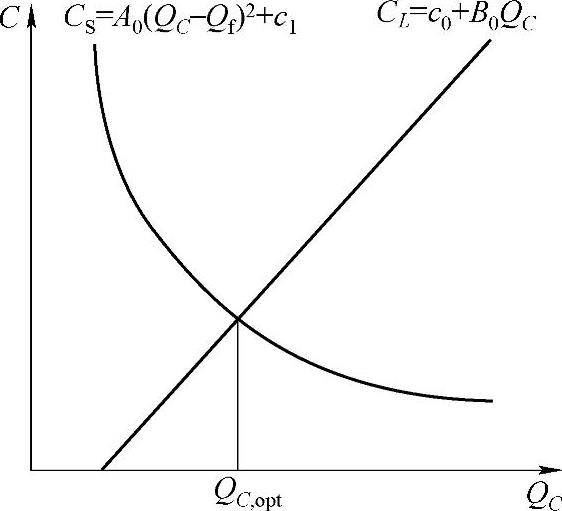
图6-5 无功规划示意图