在实际的电力系统分析计算中,从现场获取的往往都是设备铭牌参数或者设备型号,比如变压器的型号和铭牌参数、线路的型号和长度等,需要做进一步的计算才能得到建立网络模型所需的阻抗和导纳数据。但是以这种方式获得的参数与实际电力系统的设备参数值往往存在一定的差异。在实际计算过程,如果利用其进行潮流计算或者无功优化计算,计算结果会产生一定的误差。
导致计算获取的参数值与实际值之间误差的原因通常为:
1)有时因缺少实测参数量而直接采用设计参数,或者参数测量条件与实际运行条件差别较大,这都会使给定的参数值与实际运行中的元件参数有差别。
以线路参数为例,如前所述,通常情况下,现场提供的是线路型号和长度,然后根据相关公式计算线路的阻抗等参数。而参数计算同线路的敷设情况是相关的,但是线路的敷设情况在实际计算过程中是难以全面收集的,因此,大多数情况下是以某一假想的理想情况来计算的,这就使得所计算获取的线路参数同实际的参数存在差别。
又如无功补偿设备,以并联电容为例,在计算过程中往往直接利用电容的额定值进行计算。而实际电力系统中,电容所发出的无功功率值是电压的函数,其所补偿的无功功率是随着系统的电压水平而变化的。这必然会引起一定的计算误差。
2)实际运行中的元件参数因改线、改建,或因环境变化等原因而局部地、缓慢地发生着变化。
仍以变压器参数为例,如前所述,在计算其参数时,一般都利用铭牌数据计算其阻抗/导纳参数。而随着变压器运行时间的增长,相关参数必然会发生缓慢变化,此时,如果仍然利用铭牌数据换算参数将必然造成计算参数的误差。例如,同样型号的变压器,在其使用5~10年以后,对应的电气参数同刚出厂时相比必然是会有所不同的。
3)调度中心对运行中的自动调压变压器的分接头位置或补偿电容器的组数掌握得不一定确切。特别是输电线路,一般给定的参数值是在理想情况下的,但是由于温度等原因,线路实际情况与理想情况有时相差很大,因此,一般给定的线路参数值和实际值相比大约有25%~30%的误差。
错误的参数值会造成以下一些结果:
1)参数错误对所包含错误支路参数的状态估计量值产生较大的误差,从而影响其他一些应用,如安全分析等;
2)一些在正常范围内的测量值因与网络参数不一致而被检测成坏数据;
3)长期的误差使运行部门对状态估计的结果失去信心;
4)直接使用给定的参数值减弱了状态估计检测和辨识坏数据的能力;
因此,电力网络参数估计在电力系统分析中得到越来越多的关注,与状态估计和拓扑估计一样变得重要。电力网络参数估计大致可以分为以下两种方法:
1)基于残差和量测误差之间关系的灵敏度分析,这种基于灵敏度分析的状态估计与参数估计,采用常规的状态变量向量,在状态估计结束后再进行参数估计;
2)基于增广矩阵的估计,又可以分为基于常规方程的增广矩阵估计和基于卡尔曼滤波原理的增广矩阵估计两种。基于常规方程的增广矩阵估计方法受权重影响较大,而且问题的规模被扩大,降低了计算效率,此方法适用于估计值为常量的参数;基于卡尔曼滤波原理的增广矩阵估计方法一般认为后一时刻的值等于前一时刻的估计值,但如果负荷变化比较快时,此方法的收敛性较差,适用于估计值随时间变化的参数。
以上方法的参数估计准确性与量测值有很大关系。如果量测值较准确,则估计后参数精度比不估计的高;如果参与估计的线路参数初值较准,而量测值不准,则估计后误差更大。若与可疑线路有关的不良量测值未被检测出来,则参数估计值精度不高。
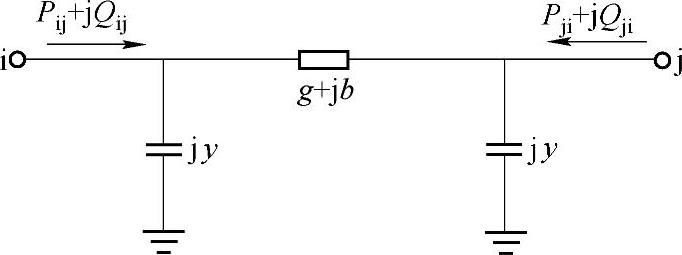
图1-7 输电线路的π形等值电路
除进行参数估计以外,还可以利用SCADA系统所获取的潮流数据对电力网络参数进行反推计算。以π形等值电路参数的反推计算为例,如图1-7所示,其中的阻抗支路参数以导纳进行表示。
阻抗支路首端和末端功率分别为
S1=Pij+j(Qij+U2iy) (1-12)
S2=Pji+j(Qji+U2jy) (1-13)
阻抗支路电流幅值为
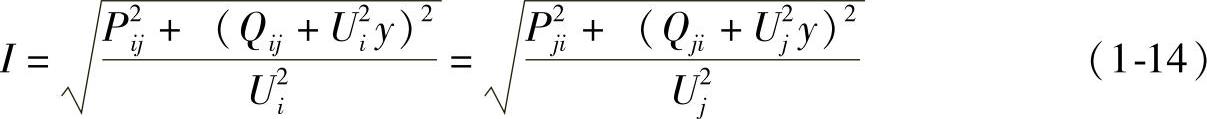 (www.daowen.com)
(www.daowen.com)
若Ui=Uj=U,则将式(1-14)整理后有

若Ui≠Uj,经整理得
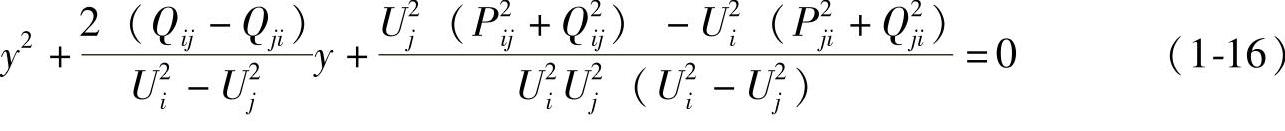
作为一个实际运行系统,该一元二次方程一定有解:
若Qij-Qji=0,则
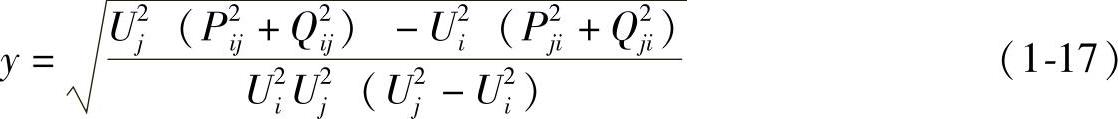
若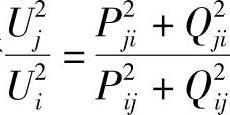 ,则
,则

若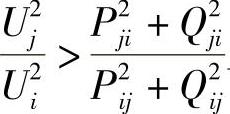 且
且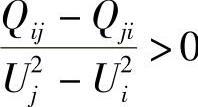 ,则
,则
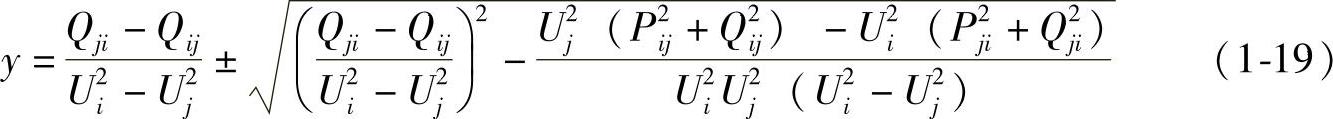
若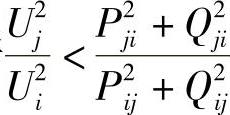 ,则
,则
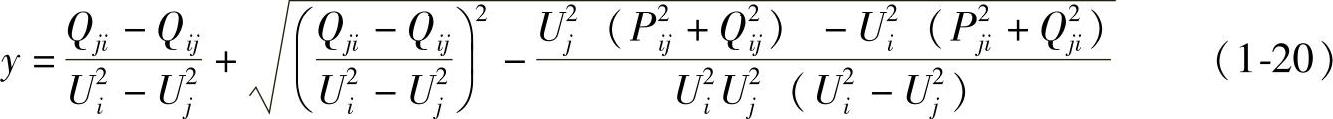
阻抗支路中的功率损耗:
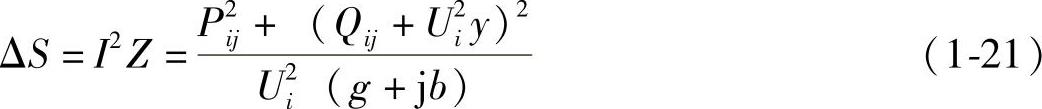
又有
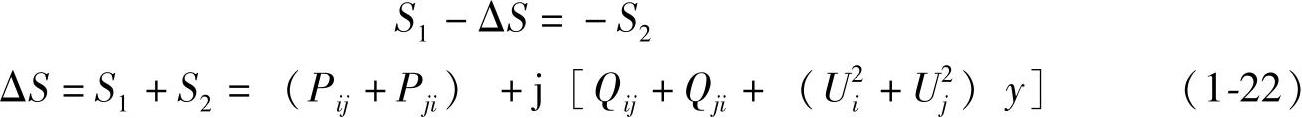
比较式(1-21)和式(1-22),令实部虚部相等,得到
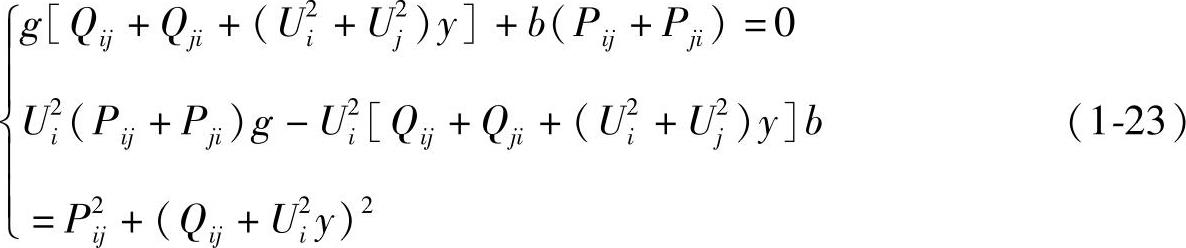
经过求解可得
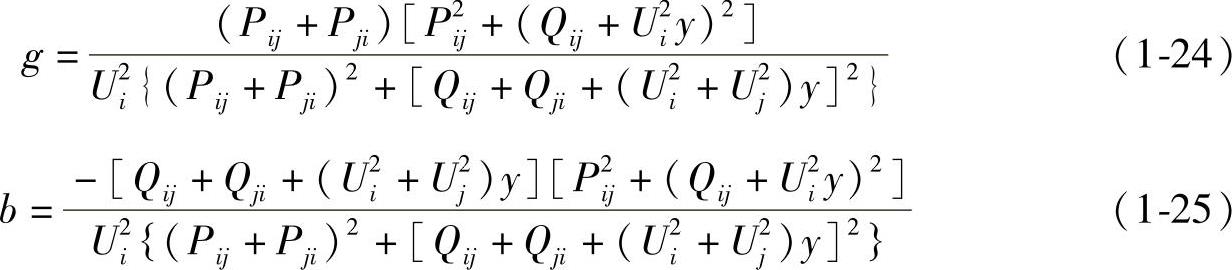
上述计算公式是从一个样本数据中得到的,计算的精度取决于样本数据的精度。为了消除样本数据误差的影响,可以采用最小二乘算法,也可以采用多个样本数据分别进行计算,然后加权平均。
线路两端潮流和两端电压幅值都是电力系统常规量测值。根据这些量测值,利用式(1-15)~式(1-20)可求得线路π形等值模型的并联对地导纳y。将导纳值代入式(1-24)、式(1-25)可以计算出模型阻抗支路的导纳值,从而得到模型参数的准确数值解。由不同时间断面的SCADA量测数据,经过求解可以得到多组线路参数的计算值。经过统计分析可以发现,这些结果大致上符合正态分布。对参数的计算结果进行正态分布估计,所得到的正态分布均值即为线路参数的最终辨识结果。
应该说明的是,上述计算所用的样本数据是历史数据,并且没有考虑变压器的电压比,也就是说,变压器的电压比隐含在线路参数中。在实际的电力网络分析中,当采用被估计的参数时,也可以不考虑变压器的电压比。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







