1.高斯法

高斯法是将叶型曲线分段后用高次曲线近似代替来计算叶片截面几何特性的，其区间不等分，叶型中间分得大，两端分得小，如附图5-1所示。

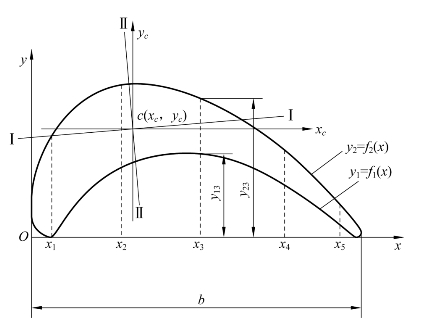
附图5-1　叶片截面几何特性高斯法计算图

高斯公式的一般形式为

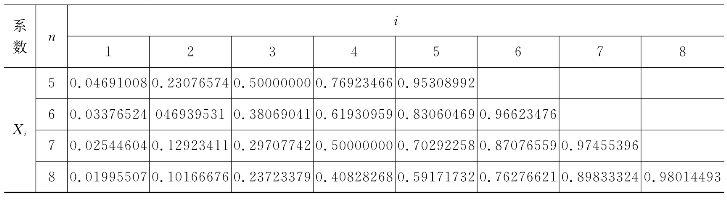
式中：Ai为与分段数有关的系数，见附表5-1；xi为分段点的横坐标，xi=bXi；b为叶片弦长；Xi为相对横坐标系数，见附表5-1；n为纵坐标数目。

附表5-1　高斯公式系数

续表

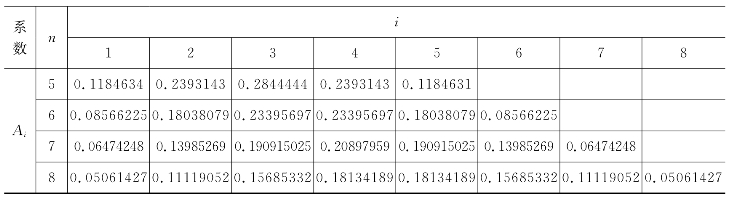
计算时，先将叶片图形放大，一般将动叶放大10～20倍，静叶放大5～10倍，以叶型进、出口连线为x轴。沿x轴将叶型分为n段（一般n=5～10已够准确），根据n在附表5-1中查出Xi，算出i点的横坐标xi，在横坐标上标出，过分段点xi作垂线交叶型内弧与背弧，量出各相应交点的纵坐标，y1i=f1（xi），y2i=f2（xi）。然后按下列公式计算叶片截面的几何特性参数。

面积：

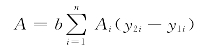
静矩：

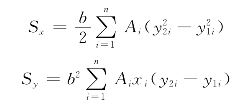
重心坐标：

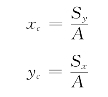(www.daowen.com)

惯性矩：

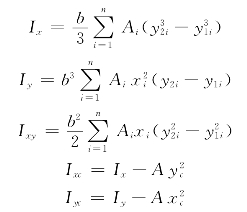
通常可简化认为

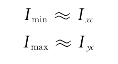
2.梯形法

梯形法是用阶梯形直线近似代替叶型曲线进行叶片截面几何特性计算的。计算过程与高斯法类同，先将叶型放大，然后将弦长等分为n段，量出各点xi处相应的叶型内弧和背弧上的纵坐标yi1和yi2，用下列公式计算。为提高计算的精确度，一般n取得较大（n=20～30）。

面积：

静矩：

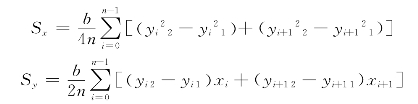
重心坐标：

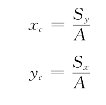
惯性矩：

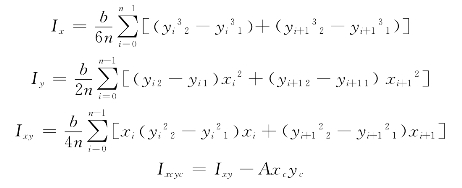
通常可简化认为

梯形法适用于计算机计算。