1.叶片与轮缘的结构

有限元分析的第一步，是要建立合理的几何模型。对于还没有三维CAD模型的零部件，可以根据二维结构图纸进行几何建模。这里分析所依据的数据资料参见图6-9。图中标示了叶根、轮缘、叶型、围带、销钉的结构和尺寸。由图可见，该级叶片的标准叶片为倒T形外包小脚叶片，采用周向方式安装在轮缘上，末级叶片叶根与其他叶根不同，采用两根锥度为1∶100、直径为13的销钉固定在轮缘上。

由CAD图可知，该级叶片的叶型部分不具有直叶片的特征，叶片自带围带，叶片整体具有不对称特征。

2.叶片与轮缘的静强度分析

1）几何模型

汽轮机叶片周向有130个叶片，周期循环对称，对于标准叶片，理论上可通过对一个基本扇区的建模分析获得全周的应力分布。图6-10是汽轮机标准动叶片及轮缘的CAD整体模型。标准动叶片由围带、叶片和叶根组成，叶根采用了双倒T形叶根。计算采用的几何模型在几何特征上基本忠实于原设计图纸。

2）网格独立性

有限元分析依赖于网格方案，网格细化到一定程度后，网格尺寸不再是有限元分析结果的影响因素，这叫作网格独立性。网格方案中，一般比较关注应力梯度较大的地方，应力梯度越大要求网格尺寸越小。

应建立不同网格数量级的叶片网格方案，比较云图中应力变化的平滑程度及应力集中处应力随局部网格密度的变化规律，一般在应力变化比较平滑、关键位置应力随网格密度变化不大的情况下，网格方案可接受。

这里最终方案没有采用四面体网格划分方式来处理模型，而是采用六面体网格，网格数目在三万左右。相对四面体网格而言，同等数量条件下，结构化六面体网格的密度和对分析对象的结构特征模拟情况将更好。

3）材料模型与边界条件

经过前期的验证和网格敏感性分析，以及处理有限元接触问题的需要，最终选用图6-11所示的有限元网格方案。图6-11给出了汽轮机转子叶片一个基本扇区模型。采用八节点六面体单元分别对围带、叶片、叶根、轮缘进行网格划分，然后将围带、叶片和叶根采用GLUE（粘接）命令连接成整体。叶片整体和轮缘采用一般接触模式。采用结构化网格，经初步力学分析，在接触区域对模型网格进行进一步优化。200 mm级标准动叶片的单元数目为31897，节点数为40211。

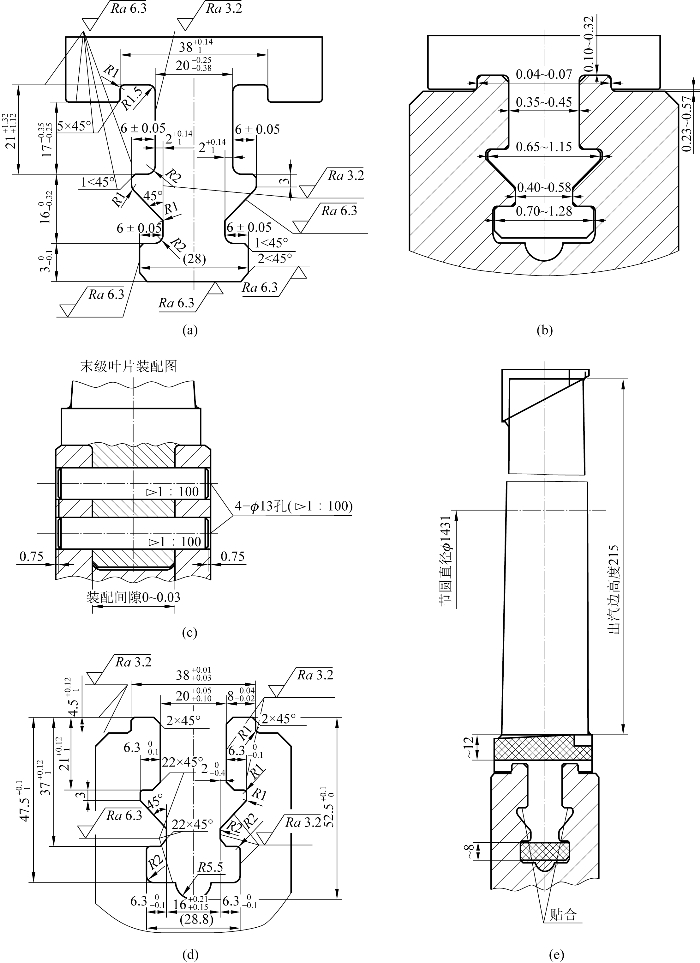
图6-9　叶片结构尺寸

（a）标准叶片叶根；（b）标准叶片轮槽；（c）末级叶片叶根装配；（d）标准叶片叶根与轮槽的配合；（e）标准叶片与轮槽的配合

图6-10　标准动叶片一个基本扇区的CAD模型

图6-11　标准动叶片一个基本扇区有限元网格模型

表6-3中给出了实际所用材料的参数，计算时参考相关数据，由于叶片处于汽轮机低压级，材料参数取温度为200 ℃时的材料性能参数。

表6-3　叶片与轮缘材料的物理和力学性能参数

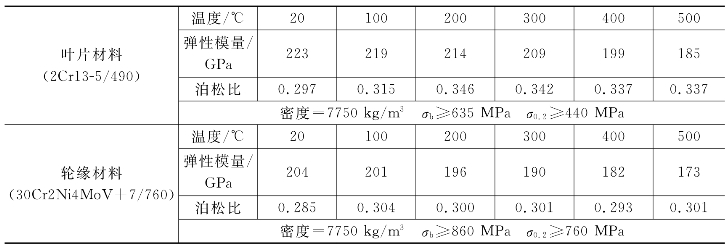
注：叶片材料参考《火力发电厂金属材料手册》，P720～P721，钢材类型为≤φ250的热轧、锻制棒，热处理过程参见《火力发电厂金属材料手册》。
轮缘材料参考《火力发电厂金属材料手册》，P572。
①分别考虑三种转速3000 r/min、3360 r/min和3600 r/min工况下的离心载荷。
②由于循环对称，约束扇区模型两个侧表面的周向位移。
③轮盘底端轴心处对一节点采用三向固定约束。
④叶片和叶根之间采用GLUE（粘接）方式接触边界。

4）弹性应力分析与结果

图6-12至图6-14给出了标准动叶片在转速为3000 r/min工况下，叶根和轮缘的应力分布。在以下的分析中，如无特殊说明，均采用笛卡儿坐标系，应力单位为Pa，空间长度单位为mm。其中，x方向为汽轮机轴向，y方向为转子径向，z方向为转子周向。

图6-12至图6-14显示，在转速为3000 r/min时，叶根最大Von Mises等效应力为414.7 MPa，轮缘最大Von Mises等效应力为366.5 MPa。为了更加清晰地显示应力的分布状况，在图6-13中，将叶根和轮缘沿图中画线处切片，如图6-14所示。从图6-14中可以看出，尽管在叶根表面接触区域应力较大，但应力递减梯度也很大。从图6-14（b）中可明显看出，叶根表面应力大于300 MPa的区域厚度不到1 mm。

图6-12显示了叶根和轮缘的Von Mises等效应力分布，其中图6-12（a）中叶根最大等效应力位于进汽侧的上T形齿过渡处；图6-12（b）中轮缘的最大等效应力同样位于进汽侧，位置在下T形齿对应的过渡处。

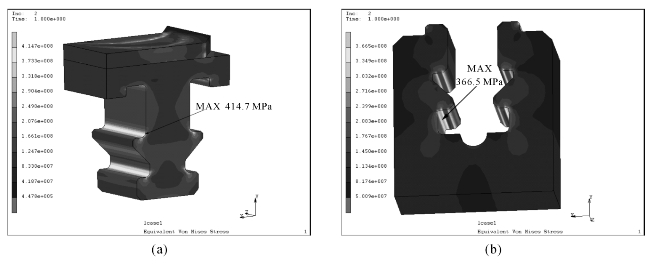
图6-12　叶根和轮缘的Von Mises等效应力分布

（a）叶根部分；（b）轮缘部分

图6-13显示了装配后的叶根轮缘总体应力分布，最大应力为叶根进汽侧的上T形齿过渡处，也就是说叶根的安全性要差于轮缘的。

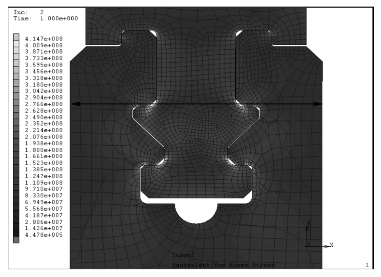
图6-13　叶根轮缘的总体应力分布

图6-14显示了装配后的叶根轮缘在某一截面上的应力分布，结合图6-15可知在该截面上，边缘处材料的应力梯度较大，其余大部分的受力水平较低。

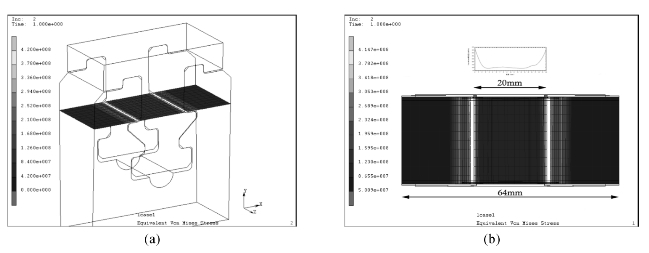
图6-14　叶根轮缘的Von Mises等效应力分布在大应力平面的切片

（a）三视图；（b）俯视图

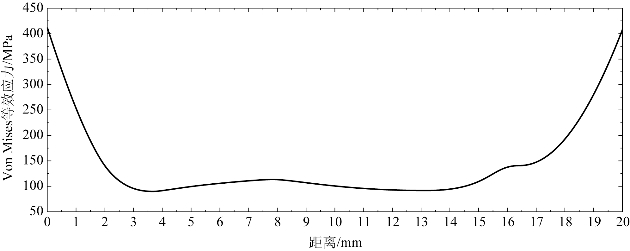
图6-15　叶根部分切片平面上Von Mises等效应力分布

图6-16至图6-20中给出了叶根和轮缘在离心力作用下所受拉应力、剪应力及表面接触正应力分布。

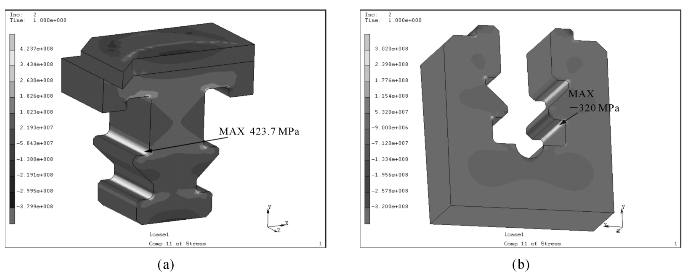
图6-16　叶根和轮缘的拉应力σxx

（a）叶根部分；（b）轮缘部分

图6-16显示了轴向应力分布状态，由图可知叶根、轮缘应力集中较为明显。

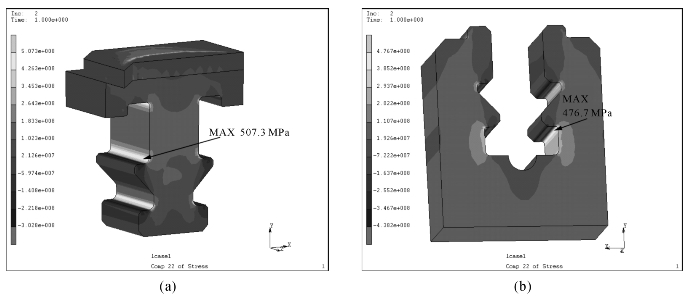
图6-17　叶根和轮缘的拉应力σyy

（a）叶根部分；（b）轮缘部分(www.daowen.com)

图6-17显示了径向应力分布状态，由图可知叶根、轮缘应力集中较为明显。位置与图6-16显示的一致。

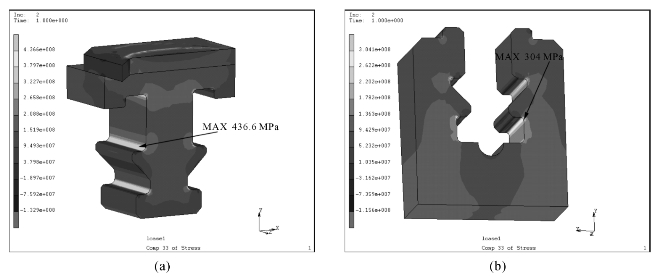
图6-18　叶根和轮缘的拉应力σzz

（a）叶根部分；（b）轮缘部分

图6-18显示了周向应力分布状态，由图可知叶根、轮缘应力集中较为明显。位置与图6-16、图6-17显示的一致。

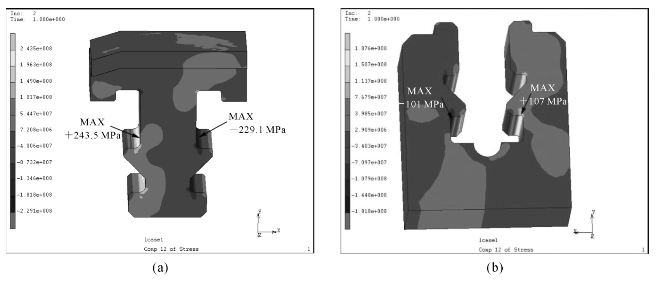
图6-19　叶根和轮缘的剪应力τxy

（a）叶根部分；（b）轮缘部分

图6-19显示了xy方向剪应力分布状态，由图可知叶根、轮缘应力集中较为明显。位置与图6-16、图6-17显示的一致。叶根应力集中处剪应力大于轮缘应力集中处的。

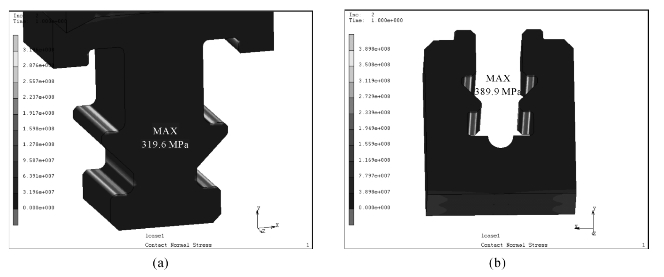
图6-20　叶根和轮缘的表面接触正应力分布

（a）叶根部分；（b）轮缘部分

图6-20显示了叶根、轮缘接触处的应力状况。由图可知接触良好。

综合图6-16至图6-20可知，在额定转速状态下，叶根关键位置处应力水平较轮缘处的要大，危险性要高，但均在安全范围内。

5）简单弹塑性应力分析与结果

以上数值分析采用的是纯弹性材料模型，并未考虑材料的塑性特征。在叶片的实际使用过程中，局部应力集中、点接触等因素很可能会导致局部位置处的材料应力超过弹性极限而使材料进入一定程度的塑性状态。局部的塑性屈服将使材料发生硬化，同时导致更多的材料承受载荷，从而使应力集中现象有所缓解。因此，前述纯弹性分析产生的特别大的应力值实际上将不会出现。

为了分析塑性对计算的影响，特别是小范围局部塑性屈服对整体应力再分布的影响，本部分拟在计算中考虑材料的弹塑性特性。由于难以获得材料的真实应力应变关系，在计算中假设材料符合理想双折线弹塑性本构关系。

表6-4给出了双折线弹塑性应力应变关系的特征点数据，表中数据假设屈服强度对应的总应变为0.2%，断裂强度对应的总应变为20%，三点之间线性过渡。

表6-4　双折线弹塑性应力应变关系特征点数据

图6-21和图6-22给出了假设的叶片和轮缘理想双折线弹塑性本构关系曲线。

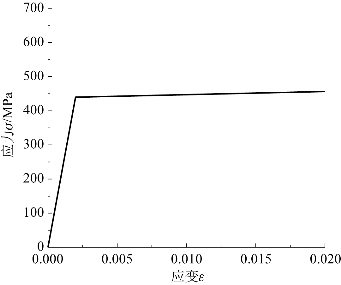
图6-21　叶片及叶根的双折线弹塑性本构关系曲线

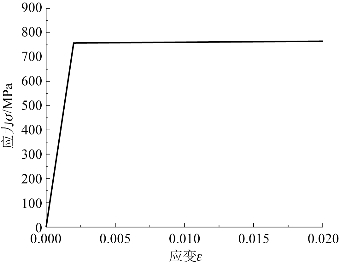
图6-22　轮缘的双折线弹塑性本构关系曲线

观察图6-23（a）中采用弹塑性与图6-13中采用纯弹性模型计算的结果云图发现，两图分布及最大、最小值完全一致。由图6-23（a）（b）（c）中应力云图分布变化情况来看，其大应力区域有增大趋势，与实际情况比较吻合。

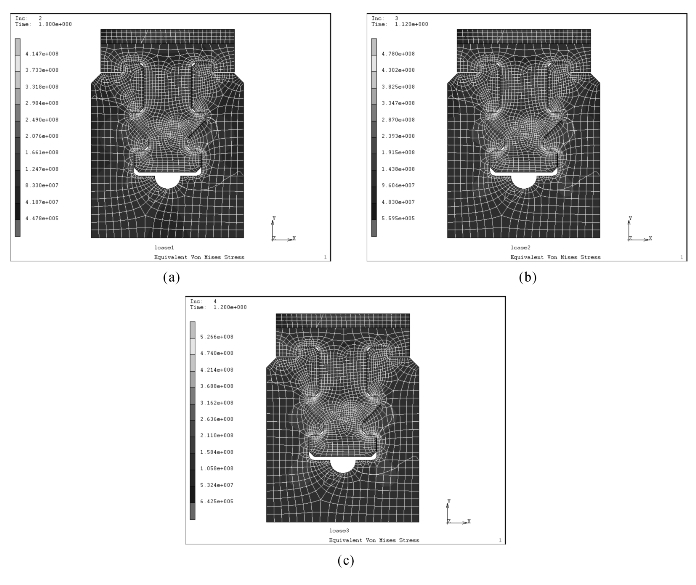
图6-23　考虑材料塑性时不同转速下叶根和轮缘Von Mises等效应力分布云图

（a）转速3000 r/min；（b）转速3360 r/min；（c）转速3600 r/min

由图6-24可以看出，在考虑塑性变形的情况下，材料所受应力在出现塑性变形后有所降低，转速为3360 r/min时，最大应力由原来的518.6 MPa降到478.9 MPa；当转速为3600 r/min时，最大应力由原来的595.3 MPa降低到526.6 MPa。从图6-24（b）可以看出，在圆角处有微小区域产生了塑性变形。图6-24（c）显示塑性区域进一步增大，但是总的来讲出现塑性变形的区域并不大。

6）计算结果的可信度分析与强度核算

应用简单的材料力学原理，求出某个特征截面的平均应力，将其与有限元计算结果进行对比，从而验证前述有限元结果的可信度。从原理上讲，在远离边界的区域，如果有限元计算的应力大小和根据材料力学原理计算的平均应力相差不大，则可认为有限元计算的结果是有效和可信的。

如图6-25所示，取图中叶片上某个截面，此截面之外的离心力全部作用到所示截面上，在转速为3000 r/min时，此截面之外离心力大小为64856.9 N，如图6-25中参数所示，截面平均拉应力为111.59 MPa。图6-26给出了此截面上的拉应力分布云图。由图可知，在远离边界的叶片中心区域，应力大小在101～108 MPa之间，与材料力学估算值差别很小，由此判断结果是可信的。

叶片和轮缘的强度核算结果如表6-5所示。

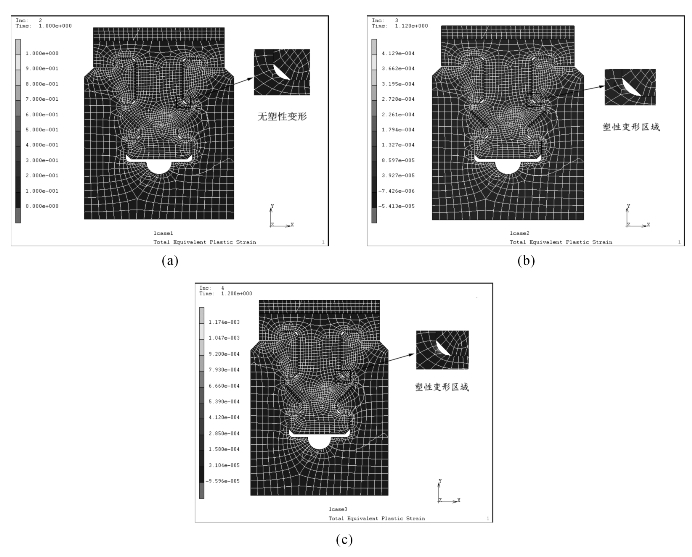
图6-24　考虑材料塑性时不同转速下叶根和轮缘等效塑性应变云图

（a）转速3000 r/min；（b）转速3360 r/min；（c）转速3600 r/min

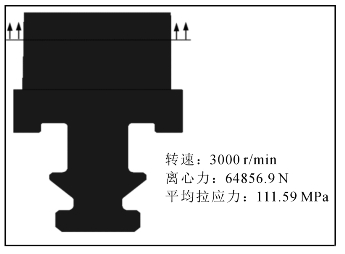
图6-25　材料力学计算的截面拉应力结果

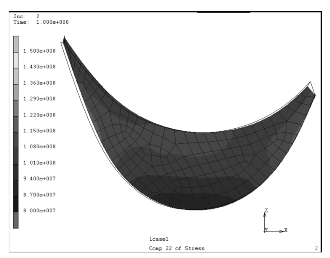
图6-26　有限元计算的截面拉应力分布云图

表6-5　叶片和轮缘的强度核算结果

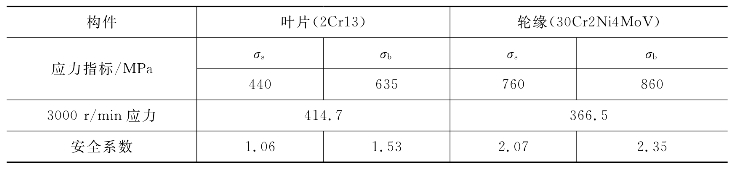
续表

由表6-5汇总的计算结果可以看出，在三个转速下应力的最大值均相对较大，尤其在转速为3600 r/min时，最大应力已经超过材料的屈服强度（但均低于抗拉强度指标）。但是由图6-26可以看出，尽管在叶根和轮缘表面接触位置处应力较大，但结构应力整体水平并不高，在图6-26 中，只在边缘非常小的区域（1～2 mm）内此切片截面的最大应力超过400 MPa，结构的应力大致在100 MPa左右。以上说明了只在应力较大的很小的区域内出现了塑性变形，应力总体水平并不高。所以，对于标准动叶片，总体而言目前的设计方案可以保证安全性。