1.初始数据

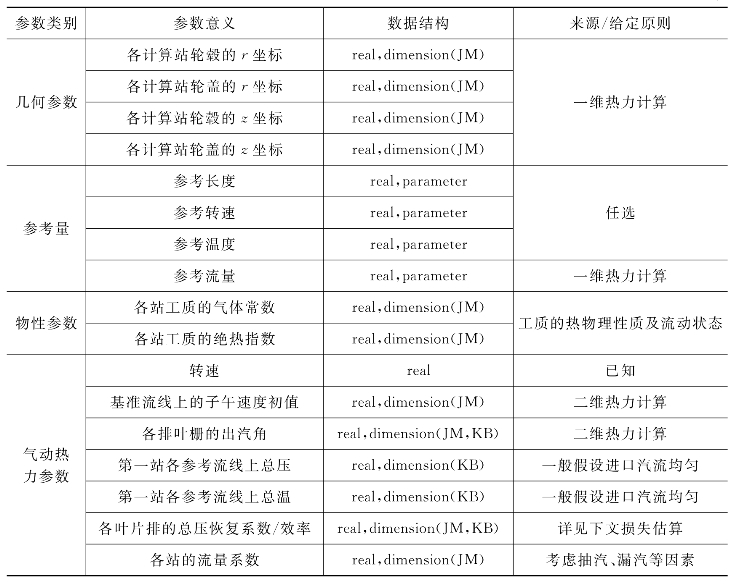
程序所需的全部初始参数如表5-11所示，可按参数类别整理成txt文件，使用Fortran程序调用时方便、清晰、容易修改。

表5-11　初始参数

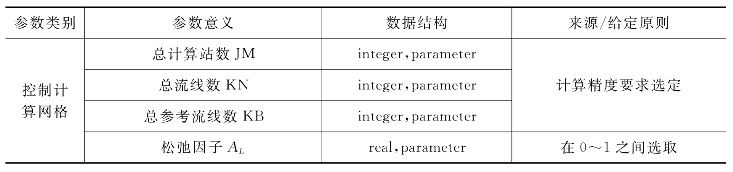
续表

2.参数的无量纲化

为使程序在各种情况下都能保证有一定的计算精度，常对物理量做无量纲化处理。量纲体系必须包括温度、长度、时间及质量4个基本量的量纲，本程序中取T0为参考温度、r0为参考长度、ω0为参考转速、给定流量G0为参考流量是合适的，可以派生出其他参考量。

参考速度：u0=r0ω0。参考焓：。

参考熵：。参考气体常数：。

参考压力：p0=G0ω0/r0。参考密度：。

在字母上方加“—”表示无量纲化后的量，有：

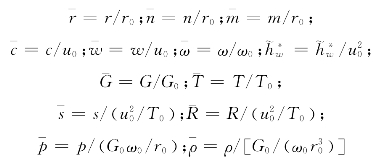
3.湿蒸汽的处理

在速度梯度方程的推导过程中，需要用到完全气体状态方程。为了使本程序能够适用于低压汽轮机，需要用完全气体状态方程的形式近似表达平衡湿蒸汽的特性，为此需要对气体常数R和比热容cp、绝热指数γ进行修改。

对于低压湿蒸汽，气体常数R可取436.5 J/（kg·K），绝热指数γ取1.063，满足适用于完全气体的式（5-25）至式（5-27）。其中，由于，则有cp=7365 J/（kg·K）。

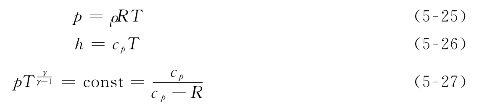
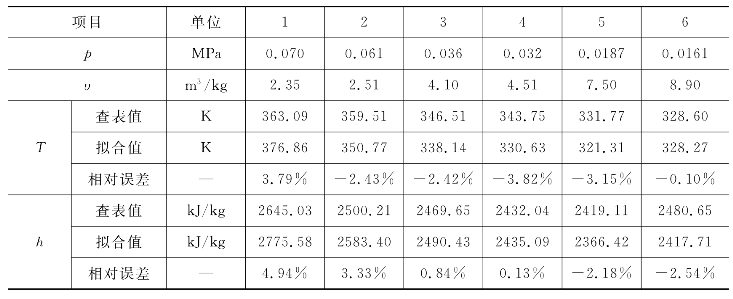
为验证对湿蒸汽做如上处理是否合适，特取作为研究对象的三排动静叶栅间隙平均截面的状态点（一维热力计算结果），比较用上述拟合方式得到的值与真实值（查水蒸气热力性质表）间的偏差，如表5-12所示。由表可以看出，曲线拟合相对误差的最大值小于5%，在工程应用可以接受的范围内。

表5-12　低压湿蒸汽曲线拟合的误差

4.损失估算

低压汽轮机内部为有黏的湿蒸汽流动，流动过程既不等熵也不等焓，所以损失系数的确定对计算结果影响较大。在准三维反问题设计中，损失估算只能采用包含经验的损失系数或损失模型。ВТИ模型适用于汽轮机低压缸，其损失的计算与叶栅的弦长、折转角、扇度、相对节距、径高比、Ma、冲角、收敛度等众参数相关，在叶片几何形状未知的反问题设计中，很多参数只能靠经验估取，加之其计算公式异常复杂，因此难以由该损失模型求得一个较好的损失估算值。因此，本章暂不采用损失模型，而是借鉴他人的设计经验给定一些较合适的损失系数，再利用总焓与总压的关系，将损失系数转化为ET（静叶总压恢复系数/动叶效率）。如果有可利用的损失模型，则只需简单地把这种损失模块外挂在程序中即可。

5.几何参数的计算

在速度梯度差分方程式（5-20）系数A1E～A7E的求解过程中，需要用到一部分几何参数，其计算方法如表5-13所示，速度分量与角度间的关系参照图5-4。

表5-13　几何参数计算方法

续表

6.气动热力参数的计算

对于S2流面各叶片排的气动热力计算来说，相对滞止转焓是一个很重要的概念，其定义式为：。它是由吴仲华先生首先提出并使用的，是准三维设计的精髓。各网格点气动热力参数的计算方法如表5-14所示，可以看出，每个网格点气动热力参数的求解均与同流线前一站网格点有关，因此第一站的总温、总压在初始条件中必须给出。

表5-14　气动热力参数计算方法(www.daowen.com)

7.三次样条插值

在数值分析中，三次样条插值是使用一种名为样条的特殊分段三次多项式进行插值的形式。它不仅能够保证各段曲线在连接点上的连续性和整条曲线在这些点上的充分光滑性，而且由于可使用低阶多项式样条实现较小的插值误差，避免了使用高阶多项式所出现的龙格现象，因此样条插值得到了广泛应用。

由数值分析的理论基础可知，唯一确定三次样条插值函数表达式s（x）的关键是确定两个边界条件。这里，根据实际问题的需要，边界条件可选取s＇（xJ=1）=s＇（xJ=2）和s＇（xJ=JM）=s＇（xJ=JM-1）。在计算过程中，需要求解一种特殊的线性方程组，其系数矩阵为对角占优的三对角矩阵，且阶数为JM，可采用“追赶法”，计算量和存储量较小。

在本程序中，三次样条插值主要运用在以下两个方面。

1）求导

（1）求各计算站各子午流线的斜率，即dr/dz。

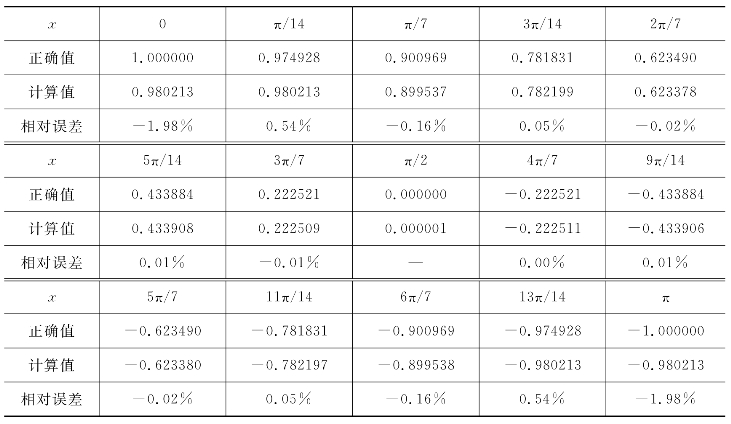
需将该流线各计算站上的离散点拟合成曲线，计算r对z坐标的一阶导数。以r=sin z（z∈（0，π））为例，选取JM个点，求导子程序的测试结果如表5-15所示。由表5-15可以看出，除始末八个点的相对误差较大外，中间点的相对误差在0.1%以内；考虑到始末八个点对应的是八个附加计算站，与叶片的设计计算没有关系，故该子程序的计算结果可以接受。

表5-15　求导子程序的测试结果

（2）求各计算站各子午流线的dφ/d m。

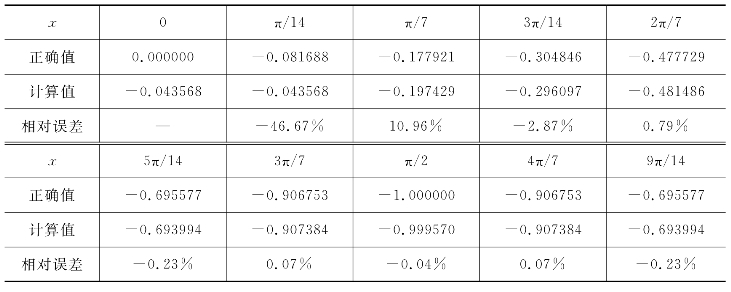
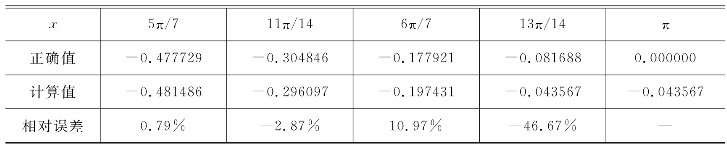
需要先求出流线的一阶导数dr/dz、二阶导数d2r/dz2，d2r/dz2是dr/dz再次调用求导子程序对z坐标求导而得。仍以r=sinz（z∈（0，π））为例，选取JM个点，求曲率子程序的测试结果，如表5-16所示。由表5-16可以看出，除始末八个点的相对误差较大外，中间点的相对误差在1%以内；考虑到始末八个点对应的是八个附加计算站，与叶片的设计计算没有关系，故该子程序的计算结果可以接受。

表5-16　求曲率子程序的测试结果

续表

2）拟合曲线求函数值

在“可控涡”程序中，分别将各子午流线上各计算站的r、dr/dz、叶片涡rVθ、子午流速wm拟合成坐标z的函数。这样在叶片内沿流线进行离散时，就可通过这些函数求出各离散点对应的r、dr/dz、rVθ、wm了。本程序利用节点处的一阶导数来表示三次样条插值函数，如式（5-28）所示，显然在函数拟合前需要先求r、dr/dz、rVθ、wm对z的一阶导数。

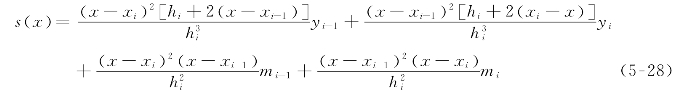
其中，x∈［xi-1，xi］，hi=xi-xi-1（i=1，2，…，n）。

8.数值积分

“可控涡”程序的核心是积分的求解。常用的数值求积方法有Newton-Cotes公式、Romberg算法、Gauss型求积公式等。Gauss型求积公式是按使代数精度达到最大的原则来选取求积节点和求出相应的求积系数的，常被称为最高代数精度求积公式。

构造任意区间［a，b］上的Gauss公式时，只要做变量置换x=（a+b）/2+（b-a）t/2，使x∈［a，b］时，t∈［-1，1］，则有

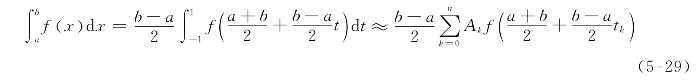
本章中，构造4个节点的Gauss-Legendre求积公式，由数值分析的理论基础可知，（n+1）个求积节点的插值型求积公式代数精度的最高值为（2n+1），因此其代数精度为7，可满足精度要求，相应的高斯点和求积系数查表可得。利用Gauss-Legendre公式编写程序求积分，测试结果如表5-17所示。

表5-17　Gauss-Legendre求积公式测试结果

9.计算数据的输出

S2流面计算程序运行后，可得到各计算站对应于要求的流量分布形式的r坐标。由于计算站的位置是确定的，这样就可以在AutoCAD中绘制S2流面的子午流线图。“可控涡”造型程序运行后，可得到各叶片各子午流线上众多离散点的（r，z，θ）坐标，可在Pro/Engineer中将叶片的中弧线绘出。由于结果均以txt文档输出，庞大的数据量会导致绘图的工作量很大，因此在后续工作中应就如何利用程序直接调用电子图板或绘图软件实现自动画图进行探讨。

在调试过程中，S2流面三个迭代层的嵌套求解对程序的稳定性要求很高，为避免出现死循环，对迭代次数做了要求，一旦达到迭代次数的上限，程序终止。同时，将三个迭代层的计算过程分别输出为txt文档，以方便对程序进行测试。