本程序主要基于S2流面理论和“可控涡”法开发，可实现汽轮机多级子午流道设计、叶片造型等功能。

程序主要包括S2子午通流设计子程序和叶片造型设计子程序两个部分。S2子午通流设计子程序是叶片造型设计子程序的先导，可为其提供初始数据。

1.S2子午通流设计程序的架构

在蒸汽透平的S2子午通流计算中，流线曲率法把一个二元问题简化为一元问题来求解，具有程序思路清晰、编写简单、占用内存少、总体计算精度高等优点。

首先，需要在S2子午流道内建立计算网格。按设计要求选定流量分布形式（如将总流量均分为N份），一般按流量和通流面积成正比的原则确定各分点，将流量相同的点用光滑曲线连接起来，就得到了初始流线。在两排叶栅间隙中与子午流线大致垂直的位置画一条直线，称为计算站。因为计算站与子午流线并非严格垂直的，因此图5-4中，φ≠ψ。

在标准的汽轮机低压缸通流设计中，对于结构上紧密连在一起的级，应尽可能做多级联算；考虑到流动的连续性及参数的相互影响，计算至少要包括三级叶片。同时，为提高数值计算的精度，特别是提高利用曲线拟合计算流线导数、曲率等几何参数的精确性，在数量有限的计算站前后各增加几站，即增加插值点的个数，这是一种行之有效的方法。这些附加计算站可视为固定不动的，无损失流道，设置出口角、绝热效率分别为90°和1。这样，初始计算网格就形成了，如图5-8所示。在整个程序的计算中，计算站是固定不变的，而流线位置将在流线迭代中不断得到修正，因此计算网格一直在变化。

图5-8　计算网格示意图

流线曲率法通流计算的核心是三个迭代层：流速迭代（内层循环）、流量迭代（中层循环）和流线迭代（外层循环），计算程序框图如图5-9所示，其中计算站序号为m，流线序号为K。

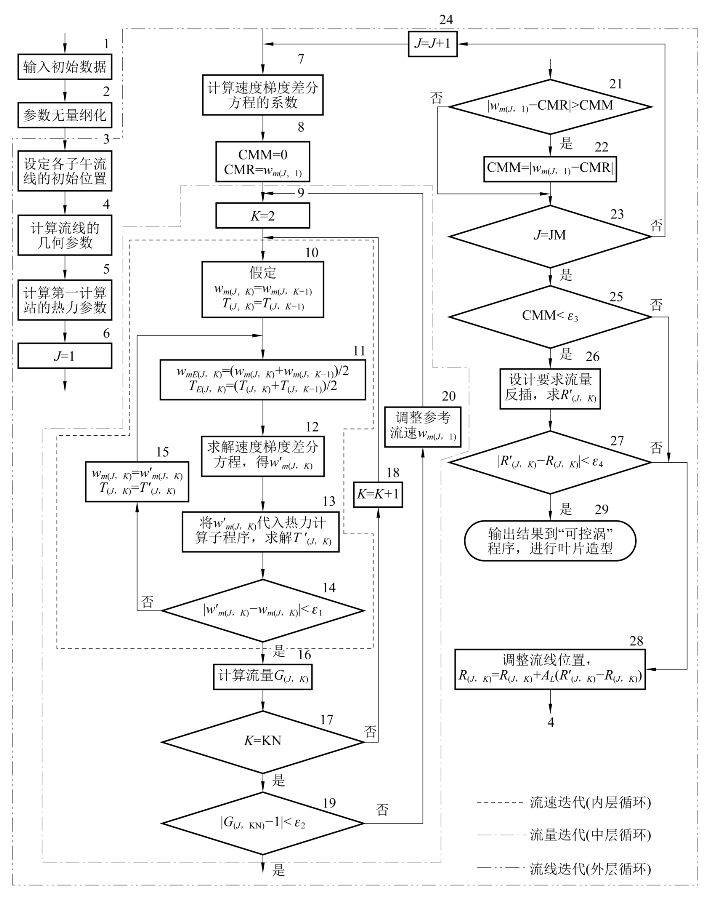
图5-9　S2流面计算程序框图

1）流速迭代（内层循环）

根据参考流线上的速度wm（J，K）（已知），利用速度梯度差分方程式（5-20），迭代计算出该站下一条流线上的速度wm（J，K+1）和相应的热力参数，这个迭代计算过程即为流速迭代。这样逐条流线推出去，可依次计算出该站各流线上的速度和热力参数。

程序实现步骤：

（1）从第一计算站开始，逐站计算各流线的几何参数（如计算站的方向角ψ、曲率dφ/dm等）和速度梯度差分方程式（5-20）的系数A1E～A7E。

（2）先假设wm（J，K）=wm（J，K-1）、T（J，K）=T（J，K-1），代入方程式（5-20）后求出w＇m（J，K）、T＇（J，K），如果小于允许误差ε1，则求解结束；否则，需将w＇m（J，K）、T＇（J，K）作为新的假设值代入差分方程中再次计算，直到前后两次流速差值的绝对值小于ε1为止。

沿计算站走向的速度梯度差分方程为

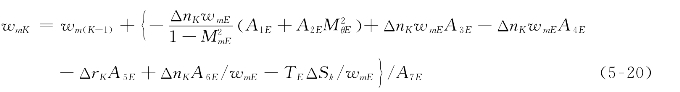
其中，

2）流量迭代（中层循环）

对于第J站，将已求出的流速代入流量公式式（5-21）中，逐条流线计算流量。根据连续方程的要求，轮盖处流线的流量G（J，KN）应为给定流量（无量纲化后为1）。记（G（J，KN）-1）为流量偏差VGG，若小于允许误差ε2，则该站求解结束；否则，说明参考流线上的流速wm（J，K）假定不合理，需调整wm（J，K）的大小，重新进行流速的迭代计算和流量计算，直到为止，此即为流量迭代。显然，流量偏差VGG随参考流速wm（J，K）的增加而增加，可视为wm（J，K）的增函数，有VGG=f（wm（J，K）），则流量的迭代问题就是求使VGG=0的wm（J，K），可采用对分区间法，如图5-10所示。(www.daowen.com)

流量公式：

式中：GK为流线K的流量；ρK为流线K的密度；wmK为计算站m流线K上的速度。

3）流线迭代（外层循环）

当完成所有计算站的计算后，初始流线位置的流量不一定能满足设计要求的流量分布形式。可将设计要求的流量分布进行线性反插，插值求出其流线在计算上对应的位置R＇（J，K），若，说明假定流线位置合理，计算结束；否则需调整流线位置，再次计算流线的几何参数、热力参数等，进行下一轮迭代计算，直到为止，此即为流线迭代。

图5-10　流量的迭代（对分区间法）

流线位置的调整方法参见式（5-22），其中引入松弛因子AL（在0～1之间取值）。由于多级联算过程中容易产生不稳定因素，且三个迭代层的嵌套求解对程序的稳定性要求很高，AL一般取较小值。

2.“可控涡”造型设计程序的架构

在S2流面计算程序运行完成后，子午面的形状就确定下来了，要想获得叶片的几何形状尚欠缺θ坐标，这就需要求解“可控涡”造型方程式（5-19）。由式（5-19）可以看出，造型设计程序的关键在于定积分的求解。数值求积分的要点有三个：积分上下限、被积函数和数值积分方法。

1）积分上下限

式（5-19）的积分变量为子午流线长度m，并不是我们使用的圆柱坐标系的某个坐标，计算起来很不方便。而m、r、wm、rVθ、dm都可以跟坐标z建立联系，是z的单值函数，因此将积分变量转换为z是合适的。这样，积分上限m对应着新的积分变量z，下限mout对应着叶片出口的z坐标zout。

2）积分表达式

原被积表达式：

在积分变量转换后，被积表达式为

在S2子午通流设计完成后，各子午流线上各计算站处的r、dr/dz、rVθ、wm均已知，运用三次样条插值方法对这些离散点进行拟合，即可得r、dr/dz、rVθ、wm对z的函数，则可得f（z）的表达式。

要获得叶片的几何形状，在求解定积分前，需要先对叶片沿z坐标进行离散，设置叶型计算点，计算仅限于叶片通道内（不含附加计算站）。造型设计程序的思路如图5-11所示。

图5-11　“可控涡”造型设计程序的思路