基于简单径向平衡法的少数几种流型在实际中经常应用，如理想等环量流型、等α1角流型等，这两种方法都比较适合采用表格的方式进行设计计算。

1.基于等环量流型的设计计算

等环量流型的设计计算相关关系式可参见5.2节相关内容，根据动叶出口角的选取方法，等环量流型设计计算有两种方法。方法1是在基元级的计算中，为获得最大的轮周效率，按经验选取β2m=β1m-（3°～5°），可得α2m=76.94°≠90°、α2≠90°，具体过程参见表5-3、表5-4；方法2是参考文献［6］，令α2=90°且沿半径不变，具体过程参见表5-5、表5-6。

由两种方法得到的速度三角形沿叶高的变化趋势可参见图5-6。

由表5-7至表5-8，可知等环量方法1中c2u≠0，而等环量方法2中c2u=0，显然方法2是理想等环量流型的“典型应用”，而方法1是理想等环量流型的近似应用，在误差许可的范围内是可以接受的。

表5-3　方法1节径截面计算

续表

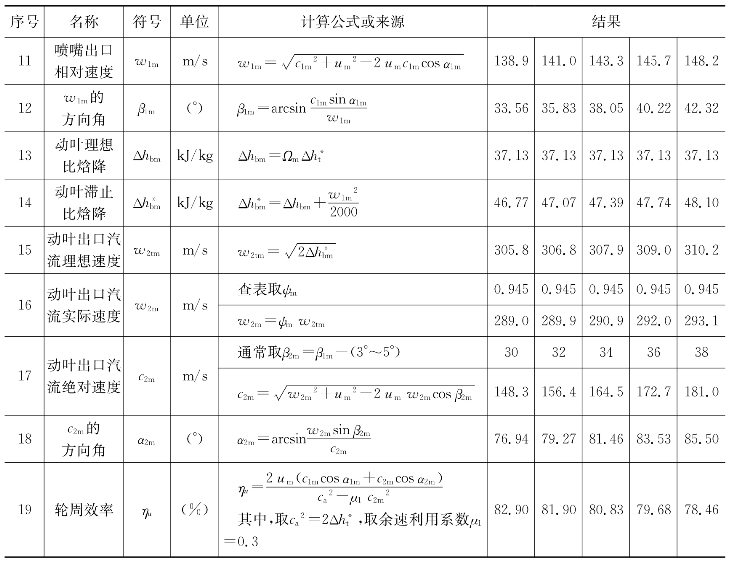
表5-4　等环量方法1计算过程

续表

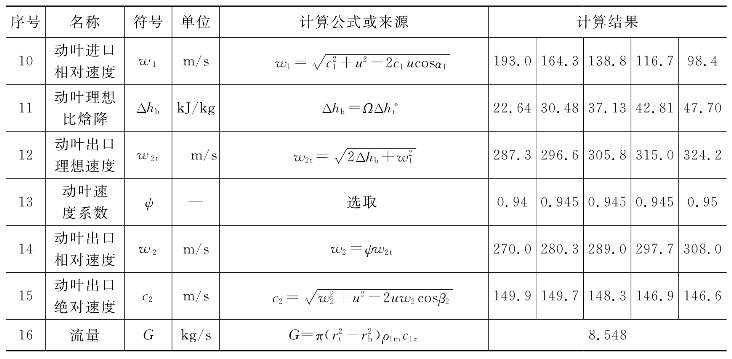
表5-5　方法2节径截面计算

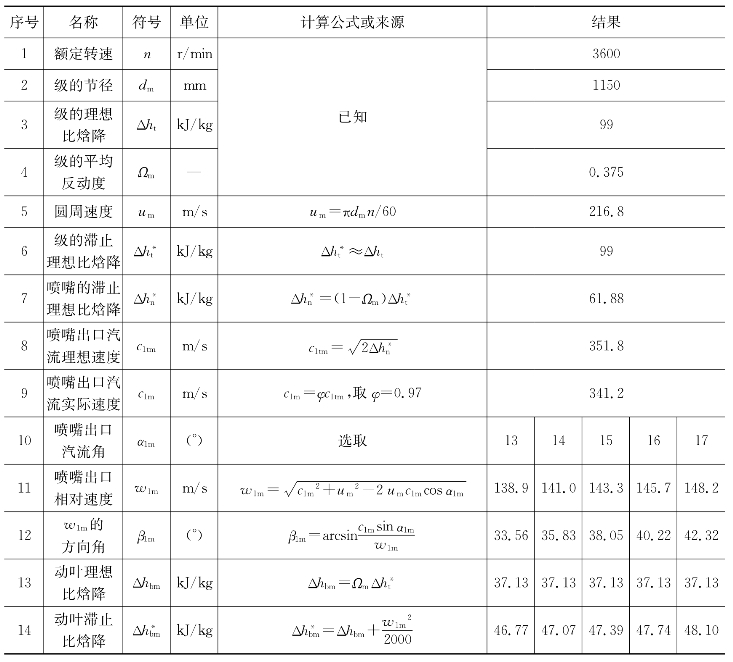
续表

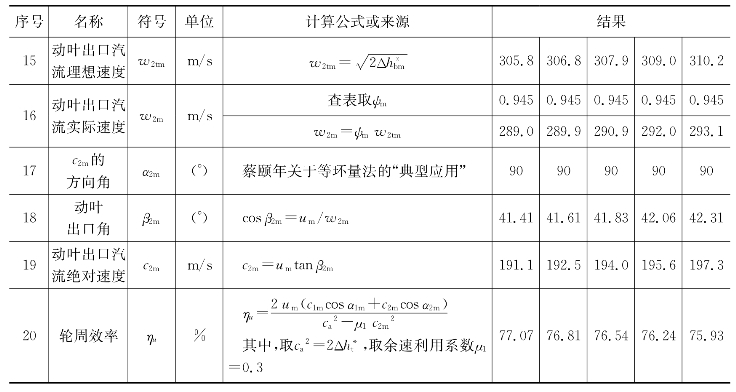
表5-6　等环量方法2计算过程

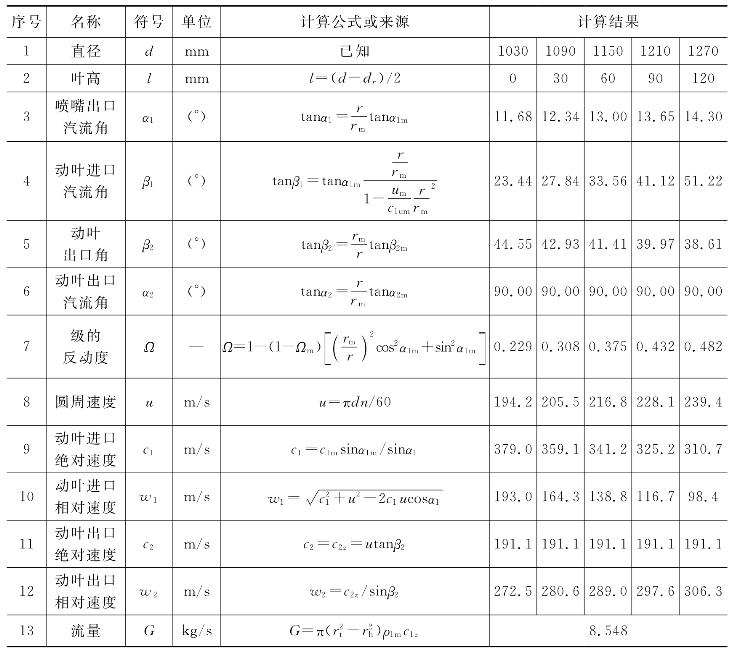
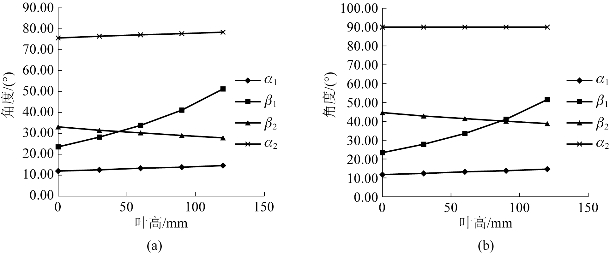
图5-6　速度三角形各角度沿叶高的变化(www.daowen.com)

（a）等环量方法1；（b）等环量方法2

表5-7　等环量方法1验证计算

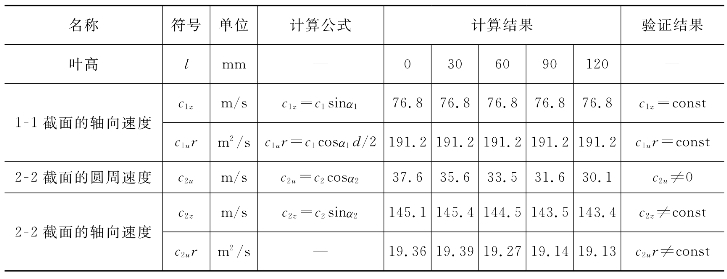
表5-8　等环量方法2验证计算

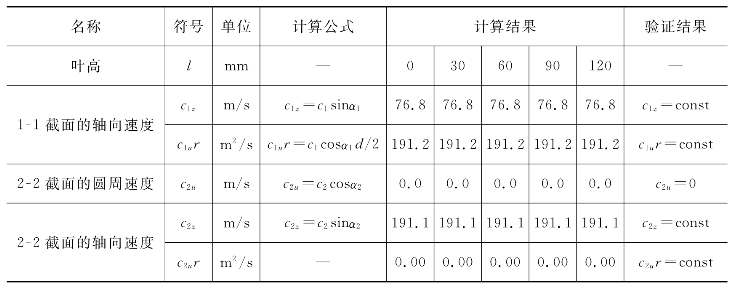
2.基于等α1角流型的设计计算

等α1角流型计算的说明：

（1）文献［5］中采用等α1角流型的透平级大都是大功率机组的末级，为了减小叶片高度，α1一般取比较大的值（20°～25°）；文献［6］在中低压部分，往往选用出口角较大的叶型，通常α1=13°～17°，本计算中按此选用。

（2）文献［6］中反动度的计算公式为。级的几何尺寸确定后，如果是粗略地估算反动度沿叶高的分布，则不管动叶出口是按哪种扭曲规律设计的（等功、等出汽角、等背压），此公式均适用。

为了便于和等环量流型比较，计算中采用蔡颐年的假设，即假定c2u=0，c2=c2z=const。

具体计算过程如表5-9所示。

表5-9　等α1角流型

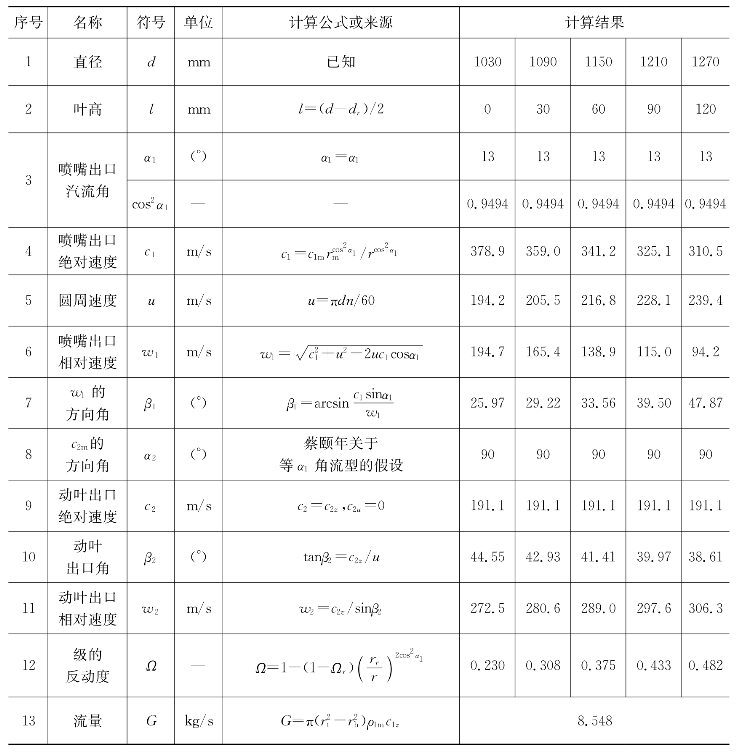
等环量方法2与等α1角流型采用相同的节径截面计算，只是长叶片的扭曲方法不同，两者的对比能代表两种流型的对比。等环量方法2中速度三角形各角度沿叶高的变化如图5-6所示，等α1角流型速度三角形各角度沿叶高的变化如图5-7所示。

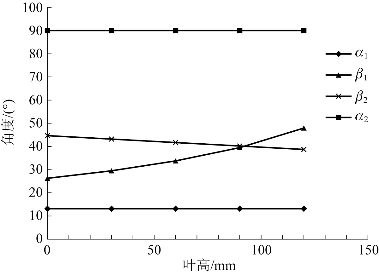
图5-7　等α1角流型速度三角形各角度沿叶高的变化

由表5-10可知，在等环量方法2中，α1=11.68°～14.30°、β1=23.44°～51.22°，等α1角流型中，α1=13°、β1=25.97°～47.87°。显然无论是静叶还是动叶，等环量流型较等α1角流型的叶片扭曲更剧烈。因此，一般认为等环量流型用于叶片不太长的中间扭叶片级较为适宜，而大功率机组的末级一般采用等α1角流型进行设计。

表5-10　等环量方法2与等α1角流型的对比

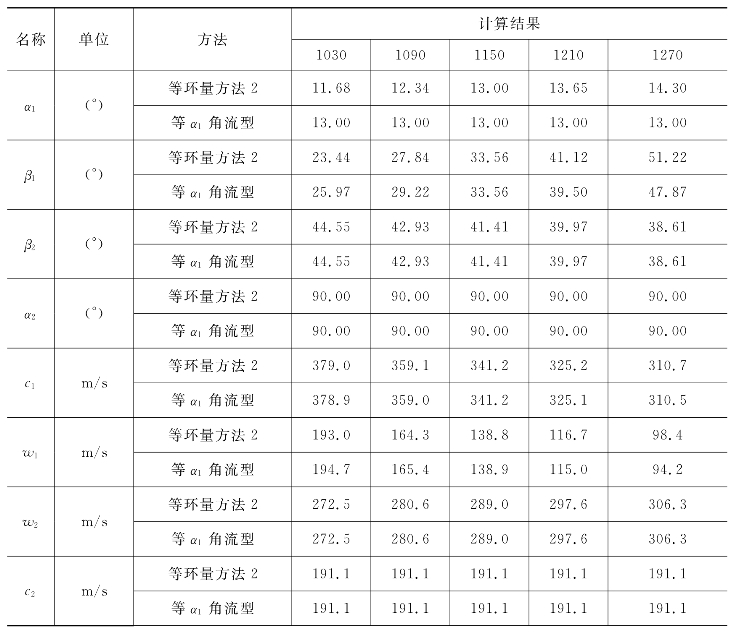
续表