1.两类相对流面理论的基本假设

透平机械内部流动是一个极其复杂的有黏、非定常、可压的真实气体流动。两类相对流面理论基于如下五个假设，将三元流场分解为两个流面上的二元流动问题来求解，简化计算。五个基本假设如下。

（1）流动是定常的。

（2）流动是绝热的，即流动过程与外界无热交换。

（3）运动方程中，忽略黏性力。

在流线曲率法中，①实际流动中黏性引起的损失可由损失模型或经验方法确定；②在固体壁面附近，由于忽略了黏性力计算得到的流速将偏高，从而导致计算得到的流量将大于实际值，可用流量系数kSJ进行修正，有kSJ=G计算/G实际。

（4）忽略流体体积力的作用。

以上假设忽略了完全三元运动方程组中的一些次要项，包含一定程度的近似，但实验表明，基于这种方法的流动与叶轮内实际流动特点相一致，忠实于原有的物理模型，能够很好地预测流动。

（5）流体为理想气体。

2.S2流面的基本方程

为建立S2流面的基本方程，采用转速为ω的旋转圆柱坐标系，各速度分量与角度间的关系如图5-4所示。

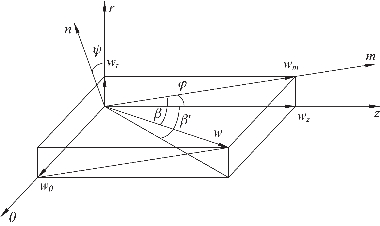
图5-4　各速度分量与角度间的关系

其中：

1）连续方程

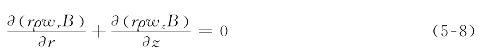
其中，角厚度B=B（r，z），是相邻两个流面之间的角距离。按两类相对流面理论，B应该在迭代中不断修正，但在本书反问题设计中，由于主要目的不在于提高流面的精确度，为减少工作量，根据叶片应力等因素所要求的叶片厚度对B进行估计。

2）能量方程

其中，相对滞止转焓的定义式为

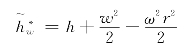
3）动量方程

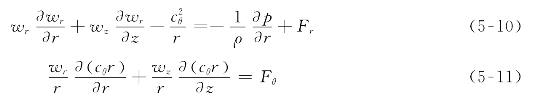
4）正交方程

5）完全气体状态方程

6）熵联系方程

7）S2流面约束方程

由于S2流面是一个连续光滑曲面，为满足“可积性条件”，则有

未知数有10个——wr、wθ、wz、Fr、Fθ、Fz、ρ、T、S、，方程有9个，需要补充一个环量分布方程：cθr=f（r，z）。方程组封闭后，给定合适的初始条件和边界条件即可求解。

3.常用的环量分布形式

在一元设计完成后，需要给定初始流线上动、静叶栅出汽角（S2流面计算程序的初参数），这就要求给出每一级的环量分布。在汽轮机设计的工程实践中，环量的分布形式经常采用的流型有理想等环量流型（也称为自由涡流型）、等α1角流型、等密流流型和可控涡流型，其中前三者的理论基础是简单径向平衡方程。

当采用简单径向平衡方程确定级的流型时，必须在动叶栅前后各补充一个条件，给定不同的补充条件可以得到不同的流型，之后用表格来计算不同叶高截面的气动热力参数，参见5.3节。图5-5所示为叶片通道的三个特征截面，下面就所用到的理想等环量流型、等α1角流型和可控涡流型的基本假设和补充条件进行汇总说明。

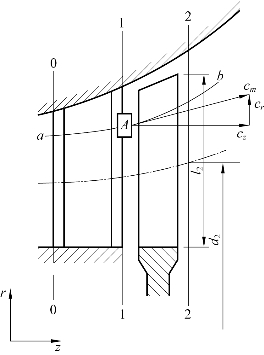
图5-5　叶片通道的三个特征截面

1）理想等环量流型

基本假设如下：

（1）忽略喷管的流动损失对等环量流型的汽流特性的影响；如需考虑，可参考文献［5］。

（2）蒸汽满足理想气体状态方程p=ρRgT。

（3）简单径向平衡法的假定——汽流在轴向间隙中做轴对称的圆柱面流动，即其径向分速度cr=0（从“密流”角度考虑，其流面并非圆柱面，这个假定不能正确地反映实际流动情况，具有一定的相似性）。(www.daowen.com)

补充条件如下：

（1）在1-1截面上，汽流的轴向分速度沿叶高保持不变，即∂c1z/∂r=0。

（2）汽轮机级的滞止比焓降沿叶高不变，即。

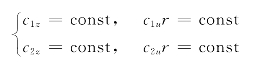
如图5-5所示，在0-0截面上汽流保持均匀的条件（特定的起始条件）下，即∂p0/∂r=0、c0u=0、c0=c0z=const，则2-2截面上的汽流也必定是均匀的，即∂p2/∂r=0、c2u=0、c2=c2z=const，否则就违反了hs=const这个补充条件。此时，动叶出口圆周速度c2u沿半径处处等于0，汽流角α2=90°，气体自动叶片流道轴向排出，余速损失最少。

等环量级参数沿径向的特点：等环量级在轴向间隙中保持了汽流的径向平衡，避免了汽流由于径向流动所产生的附加损失；扭叶片各截面型线与各相应的汽流速度三角形相适应，汽流角沿叶高的变化规律和动叶几何角沿叶高的变化规律相适应，且各基元级的气动特性与相对节距都处于较佳的范围内，从而避免了动叶进口的撞击损失和相对节距变化较大的损失；等环量级后汽流参数分布均匀，避免了级后汽流弯曲所引起的损失。由于以上这些因素，等环量级内效率较高。

由理想等环量流型的公式推导，可得出以下规律：①喷嘴出口汽流角α1沿叶高逐渐增大；②动叶进口汽流角β1沿叶高逐渐增大，且β1角的增大量比α1角的大得多，说明动叶进口边比静叶出口边扭曲得更强烈，使叶片加工较为复杂，制造成本较高；③动叶出口汽流角β2沿叶高逐渐减小；④反动度Ω沿叶高增大，易引起额外损失，当θ＜5时，这个缺点较为突出；⑤轮周功沿叶高是不变的。在级的几何尺寸和根径处轮周功相同的条件下，等环量级的轮周功率比其他流型的小。

一般认为等环量流型用于叶片不太长的中间扭叶片级较为适宜，在θ＜5时，采用其他流型更合适。

2）等α1角流型

为了避免等环量流型叶片扭曲过大，特别是喷嘴的扭曲过大的问题，提出了等α1角流型，该流型下喷嘴出口的汽流角度沿叶片高度不变化。

基本假设如下：

（1）忽略喷管的流动损失对等α1角流型的汽流特性的影响；如需考虑可参考文献［5］。（2）蒸汽满足理想气体状态方程p=ρRgT。

（3）简单径向平衡法的假定——汽流在轴向间隙中做轴对称的圆柱面流动，即其径向分速度cr=0（从“密流”角度考虑，其流面并非圆柱面，这个假定不能正确地反映实际流动情况，具有一定的相似性）。

补充条件如下：

（1）∂α1/∂r=0（或α1=const）；

（2）对于动叶出口2-2截面，存在着几种不同的扭曲方法，如

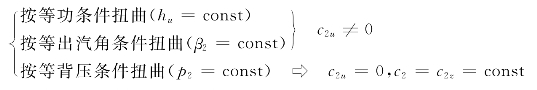
等α1角流型的反动度沿叶高的变化规律为

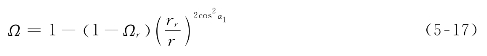
当级前汽流参数均匀，动叶出口2-2截面按等背压条件扭曲时，级的焓降hs沿半径不变。由简单径向平衡方程式（5-2），有动叶出口圆周分速度c2u=0，c2=c2z=const。

显然，这种流型的级中轴向间隙里的汽流沿叶高的流速c1u比理想等环量级的大，而c1z是沿叶高减小的。等α1角流型的轮周功沿叶高是增加的。在级的尺寸、叶片高度和叶根轮周功相同的情况下，等α1角流型的轮周功比理想等环量流型的大，但它的级内效率却较理想等环量流型的低。当α1数值很小时，cos2α1接近于1，与c1ur=常数的扭曲规律相差不大。实际上，等α1角流型由于扇形关系，角沿叶高还是略有增加的。

3）等密流流型

在汽轮机级中，蒸汽质量密度ρ与轴向分速度cz的乘积ρcz称为密流，表示通过单位面积的蒸汽流量。等密流流型就是级的密流沿径向不变。等密流流型可以实现最小的径向流动。等环量流型和等α1角流型均不能保证汽轮机级通流部分各横截面上的密流沿径向不变。

在等密流的特定条件下，汽流在喷嘴和动叶的轴向间隙中可以保持同轴的圆柱面流动，即各条子午线都是平行于轴线的；同时也保证了同一截面上喷嘴和动叶的流量相等，因而流道内的流动损失较小。但汽流沿叶高的出口速度c1z不是常数，由根部向顶部逐渐减小，从而使喷嘴出口速度场不均匀，会在轴向间隙中引起流动损失。

基本假设如下：

（1）忽略喷管的流动损失对流型的汽流特性的影响；如需考虑，可参考文献［5］。

（2）蒸汽满足理想气体状态方程p=ρRgT。

（3）简单径向平衡法的假定——汽流在轴向间隙中做轴对称的圆柱面流动，即其径向分速度cr=0。

补充条件如下：

（1）ρ1c1z=const（即）；

（2）c2z=const，c2u=0，由简单径向平衡条件，有ρ2c2z=const（即）。

理想等环量流型与等α1角流型流面并非圆柱面，并非严格遵循简单径向平衡假设，理论上等密流流型更为合理，但由于理想等环量流型和等α1角流型采用较早，积累了大量的生产经验，同时实验表明，当径高比不太小时，按这三种方法设计的长叶片级具有大致相同的级内效率，所以，目前工厂尚未广泛采用等密流流型进行长叶片的设计。

4）可控涡流型

基本假设如下：

（1）忽略喷管的流动损失对流型的汽流特性的影响；如需考虑，可参考文献［5］。

（2）蒸汽满足理想气体状态方程p=ρRgT。

（3）完全径向平衡法的假定——汽流在轴向间隙中做轴对称流动，径向分速cr≠0。

补充条件如下：

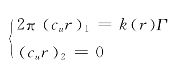
式中：Γ是设计工况下的环量，m2/s；k（r）是与叶高r对应的环量分布系数，k（r）=Ar2+Br+C。可通过调整控制点（ri，k（ri））的位置和当地值来调整整个环量沿叶高的分布。

4.特征截面的参数计算

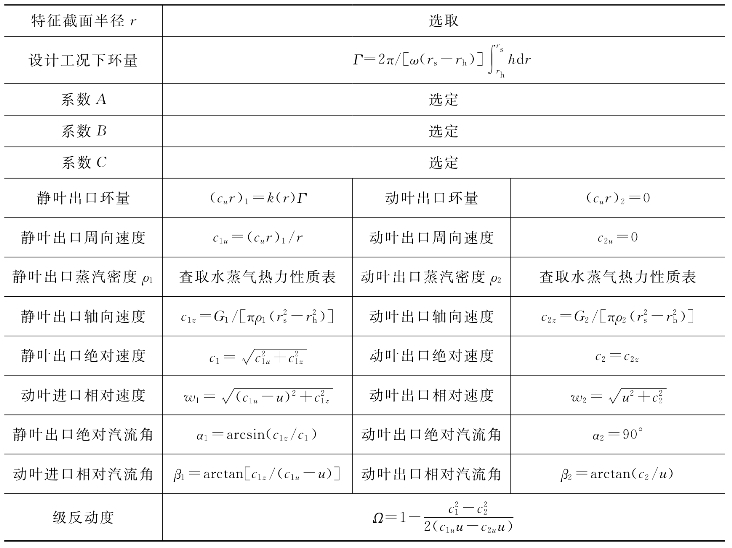
在S2流面计算程序中，需给定初始流线上各叶片排的出汽角，这依赖于各级叶栅特征截面参数的计算。理想等环量流型、等α1角流型各级叶栅特征截面参数的计算参见文献［6，7］，可控涡流型各级叶栅特征截面参数的计算如表5-2所示。

表5-2　可控涡流型叶栅特征截面参数计算