如前文所述，密相区中固体颗粒全部进入核心区，环形区中的固体颗粒是其与核心区发生质交换得到的，其质量平衡示意图如图4.8所示。

在稀相区中核心区固相的质量平衡方程可表示为：

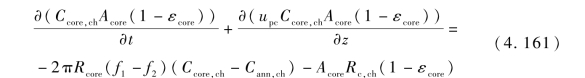
式（4.161）中，Ccore，ch为核心区的焦炭摩尔浓度；Acore为核心区的面积；εcore为核心区的空隙率；upc为核心区颗粒速度；Rcore为核心区的半径；f1为核心区向环形区的传递固体颗粒速率；f2为环形区向核心区的传递固体颗粒速率。

该方程右边第一项为环形区与核心区的质量交换项，右边第二项为核心区内发生化学反应所消耗的焦炭项。

在稀相区中环形区固相的质量平衡方程可表示为：

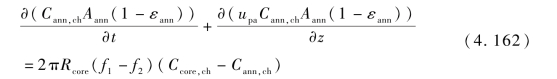(www.daowen.com)

式（4.162）中，Cann，ch为环形区的焦炭摩尔浓度；Aann为环形区的面积；εann为环形区的空隙率；upa为环形区颗粒速度。

由于假定在环形区内只有颗粒流，因此在方程中没有化学反应项。

图4.8　稀相区微元体固相的质量平衡示意图

前文中的F和F0是分别指的是床层夹带速率和床层表面处的夹带速率，是做稀相区固体质量平衡计算的初始值。具体的初始条件和边界条件参考密相区的处理。

在本书中，利用Matlab求解以上偏微分方程，首先将方程离散化得到非线性方程组，由于方程形式复杂，因此采用Newton－Raphson迭代方法进行求解。