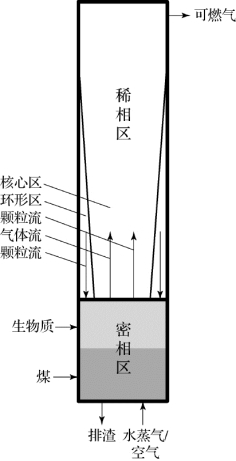
图4.6　稀相区环－核模型

稀相区内的气体和固体流动十分复杂。其模拟的方法可以采用最基本的动力学方程方法进行直接模拟。这种方法在进行局部浓度场计算时具有一定优势，但是由于气固流动的复杂性，该方法的准确性一般。另一个模拟稀相区的方法称为环－核流动（core－annulus）模型，该模型认为稀相区由两个区域组成，一是颗粒浓度较低，运动方向随着气流方向的核心区；另一个是颗粒浓度较高的、颗粒运动方向朝下的环形区，环形区内的气流速度很低。床内的气体主要通过核心区流动，具体模型的结构如图4.6所示。

本书所建稀相区环－核模型基于以下几点简化：①稀相区内的空隙率沿高度方向呈单调指数规律分布；②核心区的固体颗粒和气体来源于密相区，环形区的固体颗粒来源于核心区，是由核心区与环形区发生质交换而形成；③在核心区与环形区之间只发生固体颗粒交换，不发生气体交换，净交换量为核心区传递给环形区。

1.固体颗粒夹带率

本书中，稀相区内的固体颗粒夹带率采用Wen和Chen提出的关系式进行计算：

式（4.39）中，F（h）为密相区与稀相区交界面以上高度h处的固体颗粒夹带率；F0为床层表面处的夹带速率；F 为TDH处的夹带速率，TDH为沉降分离高度。它是稀相区的一个重要参数，若高于TDH值，则稀相区内的固体颗粒浓度不再随着稀相区高度的增加而改变；a为固体颗粒衰减指数，平均值为6.4 m－1。

式（4.42）中，u0为表观速度；ut为终端速度。计算夹带速度时，其终端速度可以按式（4.43）进行计算：

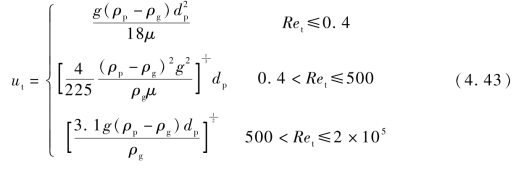
2.环形区厚度

影响环形区厚度的因素很多，如炉内的温度、气流速度、稀相区截面尺寸和颗粒的粒径大小等。本书采用Werther提出的经验公式（4.44）进行计算：

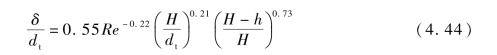
式（4.44）中，dt为稀相区截面直径。

3.核心区和环形区中气体流速

在本书中，根据Snecal提出的速度分布方程计算环形区内平均气体流速uga为：

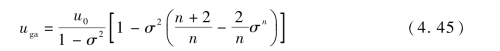
式（4.45）中，σ为核心区直径与稀相区截面直径之比；n的取值如下：

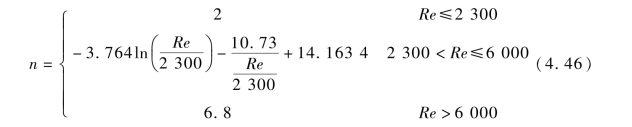
核心区平均气体流速ugc与环形区平均气体流速uga之间的关系如下：

所以核心区平均气体流速ugc为：

(www.daowen.com)

4.核心区颗粒运动速度upc和环形区颗粒运动速度upa

前文中已做相应的简化，即在核心区颗粒运动方向与气流方向相同，气体和颗粒的速度差假设为终端速度，有：

环形区内的颗粒速度upa向下，但是该速度目前无法通过理论方法得到，而是采用前人的经验数值，一般为1～2 m／s。

5.稀相区的空隙率

稀相区内的空隙率的分布在轴向和径向都是不同的，其规律十分复杂，这也是建立环－核模型十分关键的一方面。关于径向空隙率的部分经验公式，有许多研究者提出了不同的或改进的关联式。经过研究，本模型采用Zhang提出的表达式：

式（4.50）中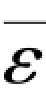，为轴向平均空隙率，轴向平均空隙率一般认为呈S形分布，即床层顶部空隙率大，为颗粒稀相区；床层底部空隙率小，为颗粒密相区。由于稀相和密相之间有一个拐点，因此本书采用李佑楚等提出的空隙率分布模型进行计算：

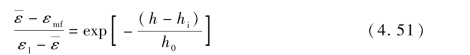
式（4.51）中的特性参数如下：

εl为稀相极限空隙率。

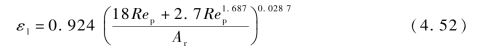
h0为特征长度。

hi为转折点高度。

up为颗粒表观速度。

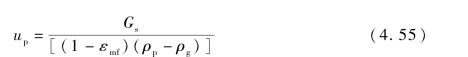
Gs为被气流携带走的颗粒量。

6.固体颗粒的径向混合

核心区向环形区的固体颗粒传递速率f1（m／s）和环形区向核心区的固体颗粒传递速率f2（m／s）采用白丁荣通过实验所拟合出的经验公式（4.56）进行计算：

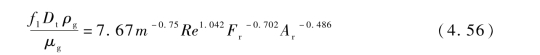
式（4.56）中，m为气固比：