1.密相区内气泡运动特性及参数

在气化炉的床层上，气流从下而上穿越床层，当气流速度较小时，气体会从颗粒间的间隙处通过，整个床层在宏观上保持一个稳定状态，固定床气化炉工作时就处于这个状态，当穿过床层的气流速度超过了其对应燃料颗粒的最小流化速度时，气体无法从颗粒间的间隙处通过，而是将以气泡的形式通过床层，这就是本书所研究的流化床气化炉的工作状态。气泡相区域的结构如图4.2所示，在流化床中，气泡在布风板的表面形成，形成之初很小，而后迅速上升，并且在这个上升的过程中，随着气泡之间的合并以及周围压力的变化，气泡尺寸将变大，上升的速率也会提高。气泡的形状在初期为较小的球形，而后逐渐变大且为扁平状，最终呈现球形帽状。气泡的存在对炉内的气化反应既存在促进作用也存在抑制作用。所谓促进作用指的是气泡在上升过程中引起的炉内物质的强烈搅动与混合，不但能增加气固接触效率，而且能保证传热过程和传质过程快速完成。对于气化反应的抑制作用指的是部分气泡中的气体会一直在气泡中，直到穿过床层进入自由空间。这部分气体不会在床层中参与反应，形成“短路”。显然，这是不利于炉内反应进行的，所以气泡的行为对于床层的传递特性（如颗粒混合、颗粒扬析、气体混合、传热、传质等）是起决定性作用的，因此在建立气化炉的综合数学模型时，应先考虑如何对气泡的行为进行描述。

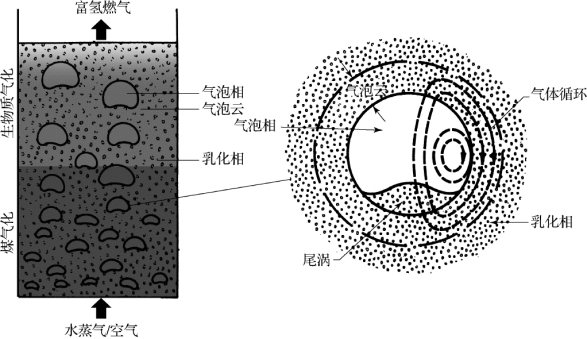
图4.2　气泡相区域的结构

针对流化床气化炉这个多气泡系统，其分析的基础是在对单个气泡分析的基础上发展而来的。下面从单个气泡的行为分析出发，逐渐过渡到多气泡流化床的分析。气泡的行为分析主要包括气泡的形状及其变化、气泡云层及其尾涡的变化、气泡直径、上升速度、气泡所占体积份额等。

如图4.2所示，气泡周边存在气泡相、乳化相、气泡云相以及尾涡区，气泡相和乳化相显而易见，气泡云是指当气泡速度大于乳化相中的间隙气体速度时，气体对流循环从气泡空隙的顶部进入乳化相，然后将气体在气泡外循环返回其下部。发生这种循环的气泡周围的区域称为气泡云。气泡的上升速度将会直接影响到气泡云的大小和厚度，以乳化相的颗粒间隙的气流速度来区分，当气泡的上升速度大于它时，气泡与乳化相之间就可以形成气泡云。这样的气泡称为有云气泡，又名快气泡。在上升过程中，气泡速度会提升，气泡云层的厚度会减薄。当气泡上升速度很快时，气泡云层的厚度将会变得非常薄。这样，气体基本只能在气泡内部循环了。在气泡的下部存在一个突起的尾涡，尾涡被认为是气泡云的一部分，它是气泡尾部的一群随着气泡上升的颗粒。由于尾涡与气泡同时上升，因此尾涡区域中的颗粒的运动速度与气泡的上升速度基本相同，与乳化相中的颗粒相比，尾涡区域中的颗粒的运动速度更大，因此，尾涡是炉内颗粒运动的主要动力，对床层中颗粒运动起到了重要的作用。

描述气泡上升的过程是十分重要的。在气液系统中和气固系统中气泡的行为有类似的表达，在气液系统中，球形气泡的上升速度可以通过戴维斯和泰勒的理论进行很好的表述：

其中Rn为气泡前端的曲率半径。

由Davidson等测量得到的气泡上升速度可以表示为：

其中db为与气泡等体积的球体的直径。

在本书的流化床气固系统中，气泡上升速度有类似的表述方式，采用式（4.3）进行计算：

其中u0为气体的表观速度；umf为流化床的临界流速；ubr为气泡上升相对速度，本书采用式（4.4）进行计算：

气泡的上升速度和气泡云相的厚度有直接关系，也直接影响到气泡直径的大小。根据气泡上升速度与乳化相的颗粒间隙气体流速的大小，可将气泡流动模式分为快气泡和慢气泡。乳化相的颗粒间隙气速uf可表示为：

其中εmf为临界空隙率。

当气泡的上升速度大于乳化相颗粒间隙的气流速度，即ubr＞uf时，在气泡相和乳化相之间就会形成气泡云相。此时，气泡就称为有云气泡或快气泡。

当气泡的上升速度小于乳化相颗粒间隙的气流速度，即ubr＜uf时，由于气流不在气泡相与周围乳化相之间循环，因此不会形成气泡云相，而是会穿过气泡。此时，气泡就称为无云气泡，或慢气泡。

气泡在床内所占的体积份额δ根据气泡的速度参考经验公式（4.6），对于慢气泡有：

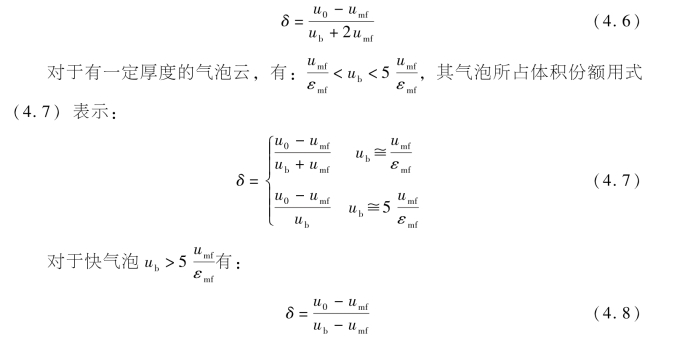
气泡云相与气泡的体积之比fc可以定义为：

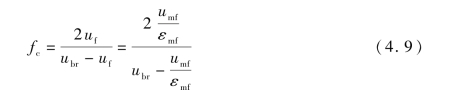
气泡的尾迹也需要在模型中考虑。图4.3所示为尾涡角度θw和尾涡与气泡体积的比值fw。气泡基本是球形，但是其底部总会有一个凹陷部位，即尾涡区域。

式（4.10）中，Vw为尾涡部分体积，该参数无法通过理论分析确定。本书根据图4.3中的经验数据得到fw，该数据是由Rowe和Partridge在X射线拍照技术下观察得到的经验值。

由于在运动的过程中气泡会合并也会破裂，所以气泡的尺寸变化十分复杂，难以用模型进行预测。目前，多采用前人所研究的经验公式进行估算。本书采用的是Mori和Wen提出的关联式（4.11）来表示：

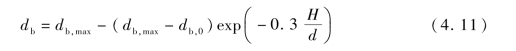
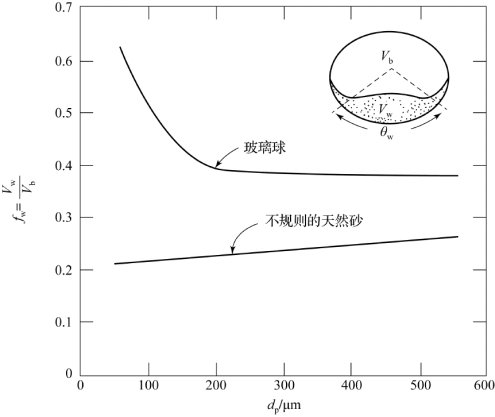
图4.3　尾涡体积与气泡体积之间的关系

式（4.11）中，d为流化床直径；db为床高H处的气泡平均直径；db，0为布风板上形成初始气泡的平均直径；db，max为最大气泡直径。

由于本书所研究对象的实验对照设备的布风板采用的是多孔板，因此在模型中也采用相应的经验公式表示，db，0用式（4.12）来表示：

式（4.12）中，AD为布风板上每个小孔所影响的区域面积，即布风板的总截面面积与孔道数量的比值。在实验对照组中，布风板的结构如图4.4所示。

最大气泡直径db，max用式（4.13）来表示：

2.密相区的特性

（1）密相区高度。

流化床中密相区的高度并非投料高度，之所以热态运行时床层将会膨胀，主要是因为乳化相会受热膨胀。另外，运行过程中会产生气泡，气泡的存在增大了料层的体积。膨胀后的床层高度Hf可通过式（4.14）进行计算：

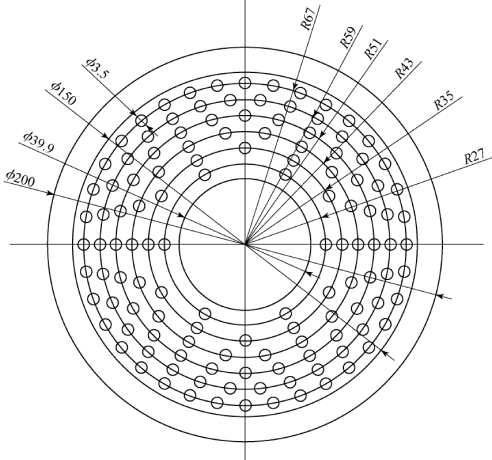
图4.4　布风板的结构

式（4.14）中，Hem为乳化相膨胀床高度。对于本书中采用的砂粒、煤粒、生物质颗粒等典型的Geldart B类颗粒，乳化相一般不膨胀，即Hem＝Hmf；其中Hmf为最小流化速度下的床层高度；δb为床层气泡相的体积分数。式（4.14）可转化为式（4.15）：

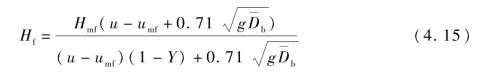
式（4.15）中，Y为修正系数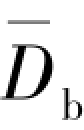，为全床层的平均气泡直径，可分别表示为以下形式：

（2）临界流化速度、临界空隙率。

临界流化速度umf可由Ergun公式得到它的二次方程：

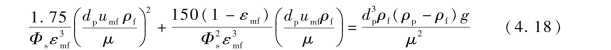
式（4.18）中，Φs为固体颗粒的球形度；εmf为临界流化状态时的空隙率，其表达形式如下：

式（4.19）中，Ar为准则关系式（Archimedes Number），该关系式包括了颗粒尺寸、颗粒物性参数与气体物性参数，表征了颗粒的流化特性。其表达形式如下：

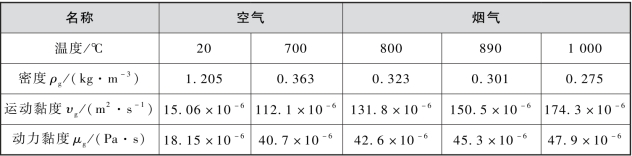
式（4.20）中，ρg为气体密度；ρp为颗粒密度；dp为颗粒的平均直径；μg为气体动力黏度。常见气体的物性参数见表4.1。

表4.1　常见气体的物性参数(www.daowen.com)

对方程（4.18）进行简化得到：

式（4.21）中，Remf为临界流速下的雷诺数，其表示为：

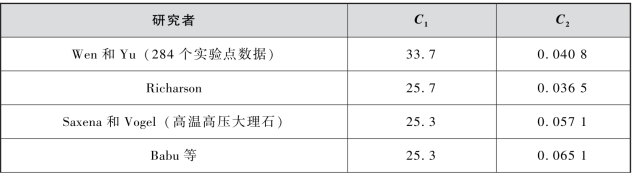
不同研究者的参数C1、C2的取值见表4.2。

表4.2　不同研究者的参数C1、C2的取值

续表

（3）颗粒终端速度。

颗粒终端速度可通过一个理想球体的受力分析得到。假设颗粒是一个自由沉降的光滑球颗粒，它所受到的力主要是重力Fg、浮力Fb和流体对颗粒向上的曳力Fd。这三个力的综合值决定了该颗粒的运动方向和速度。当Fd＝Fg＋Fb时，颗粒受力平衡，将等速降落，此时的颗粒运动速度ut称为颗粒的自由沉降速度。该速度是指颗粒相对于流体的运动速度，即颗粒终端速度。该速度可表示为：

式（4.23）中，CD为曳力系数，与终端雷诺数Ret有关，大概在三个不同的区域呈现不同的规律：

滞留区：

Ret＜0.4，CD与Ret在双对数坐标上成线性关系：

过渡流区：

Ret＝2～500，CD与Ret的关系可近似地用式（4.25）表示：

湍流区：

Ret＝500～200 000，CD趋近于常数：

根据CD曳力系数与终端雷诺数Ret的关系得到球体颗粒终端速度的解析式：

滞留区：

过渡流区：

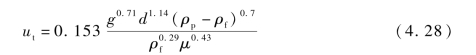
湍流区：

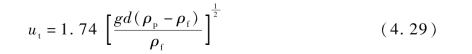
（4）密相区内固体颗粒运动特性及参数。

如图4.5所示，在密相区中，尾涡区、气泡云相和乳化相中都存在固体颗粒。这些颗粒的运动都是由气泡运动所引起的。一般认为，气泡尾部的尾涡内的颗粒会随着气泡一起上升，因此在本书中假设尾涡内颗粒的上升速度等于气泡的上升速度，即：

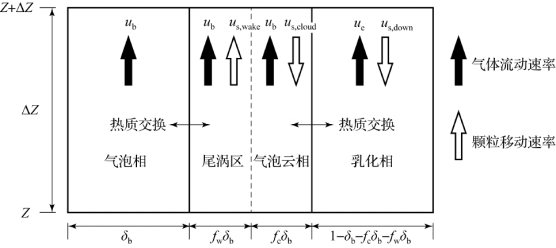
图4.5　密相区流动示意图

在本书中速度朝上时用“＋”来表示。

随着尾涡区内颗粒上升，气泡会留下空隙，这些空隙需要被乳化相和气泡云相中的颗粒填充，虽然乳化相和气泡云相还存在质交换现象，但是基于质量守恒原理，有：

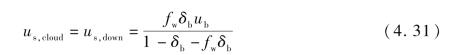
穿过乳化相的气体的上升速度可以表示为：

3.密相区模型总体介绍

两相模型是最早被提出来的密相区模型。该模型结构简单，主要将密相区划分为气泡相和乳化相两个区域。乳化相维持在临界流化状态，不能从乳化相中穿过的气体以气泡形式穿过床层。该模型过于简单，若在实验中发现了尾涡区，则气泡云相等部分在该模型中都无法体现，直接导致若使用该模型对密相区进行模拟，则会有很多现象无法解释，模型的模拟准确性无法保证。本书采用的是对两相模型进行修正后的，由Kunni和Levenspiel提出的三相鼓泡床模型，简称K－L鼓泡床模型。

图4.5所示的是基于K－L鼓泡床模型的密相区流动示意图。在该模型中将密相区划分为气泡相区、气泡云区和乳化相区，其中气泡云区又包括了尾涡区和气泡云相区。其中气泡相区所占份额为δb，尾涡区所占份额为fwδb，气泡云相区所占份额为fcδb，乳化相区所占份额为1－δb－fwδb－fcδb。

流化床中气流速度较快，一般气泡中的气体流速会高于气泡的上升速度，这部分高出的气体速度称为穿行速度，但是由于相对较小，本书中做简化处理，忽略该部分所产生的影响。假设气泡相、气泡云相和尾涡区的气体的上升速度都是ub，而乳化相中的气体流动速度用uge表示。它是由乳化相中的气固相对速度ue和乳化相中的颗粒下降速度us，down所确定的，表达式如下：

则炉内气体的表观速度u0可写为：

式（4.34）中，εc为气泡云中的空隙率，εe为乳化相中的空隙率。一般认为，若以上两个参数与临界状态下的空隙率εmf相同，则截面的气体空隙率可用式（4.35）表示：

4.不同相之间的气体交换

在本书所研究的工艺中，碳颗粒和生物质颗粒在炉内发生燃烧和气化反应。这些过程将会导致气泡相、气泡云相与乳化相之间发生大量的热质交换现象。本节主要介绍各相质交换的规律，热交换则在后面章节中介绍。

气泡相与气泡云相之间发生的质交换一部分是由气体川流引起的质交换，另一部分是由气体的浓度差引起的气体扩散，气泡相与气泡云相之间的质交换系数Kbc可表示为：

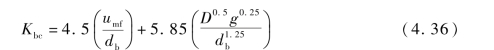
气泡云相与乳化相之间的质交换主要依靠气体浓度差所产生的气体扩散，乳化相与气泡云相之间的质交换系数Kce可表示为：

式（4.37）中，D为气体的扩散系数，用经验公式（4.38）估算，可表示为：