表达式的繁简结构和运算类型都可等效变换，有相应规则和定理保证变换的等效性。

表达式运算方式的等效转换有摩根定理保证和括号变换规则的辅助。

1.括号变换规则

表达式中的括号表示超越规则的运算，有加括号和去（也叫展开）括号两种转换内容。

（1）与、或混合运算中的括号转换

展开括号：

A（B+C）=AB+AC

在逻辑代数中称之为“与对或的分配律”。

加括号（提取公因子时，要加括号）：

AB+AC=A（B+C）

这两个等式在普通数学中已被公认，在逻辑代数中是否成立还需证明。在逻辑代数中，最基本的证明手段是真值表，证明原理是对应变量的全部取值组合，如果两个函数的运算值完全相同，则这两个函数表达式相等（即等效）。下面用表4-21所示的真值表证明它们成立。

表4-21 证明等式的真值表

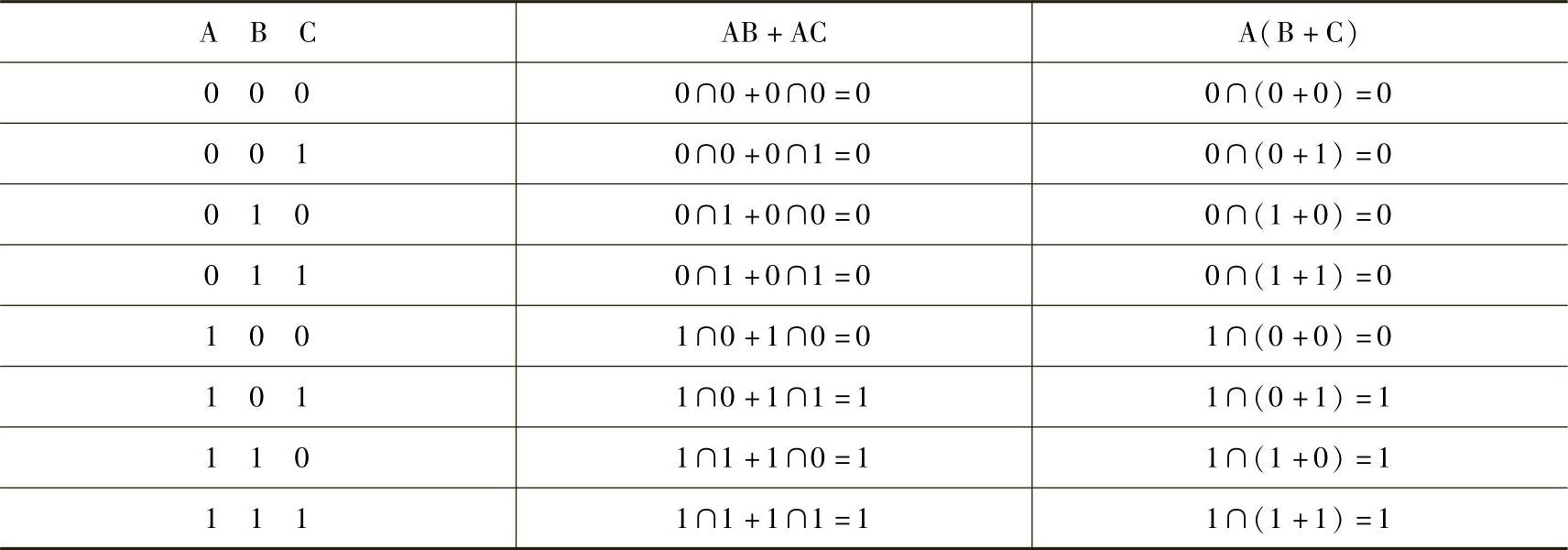
通过真值表的证明得到

AB+AC=A（B+C）

（2）与、异或混合运算中的括号转换

提取公因子，加括号：

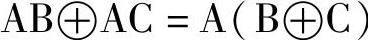
展开括号：

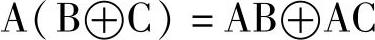
2.德·摩根定理（简称摩根定理）

揭示表达式中的与、或运算及非号的转换关系，可灵活用于表达式任何部位的运算转换。

两个变量的摩根定理转换形式：(www.daowen.com)

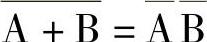
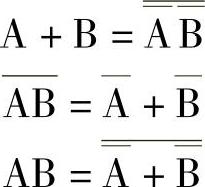
3个变量的摩根定理变换形式：

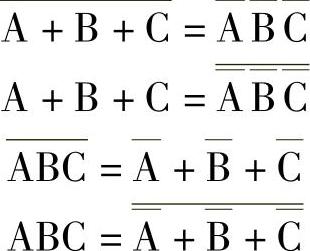
用摩根定理变换表达式运算类型，有时要加括号，以维持表达式原来运算顺序，保证变换的等效性，如：

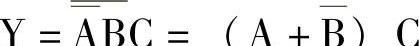
可用真值表检验表达式的等效关系，见表4-22。

表4-22 检验变换等效性真值表

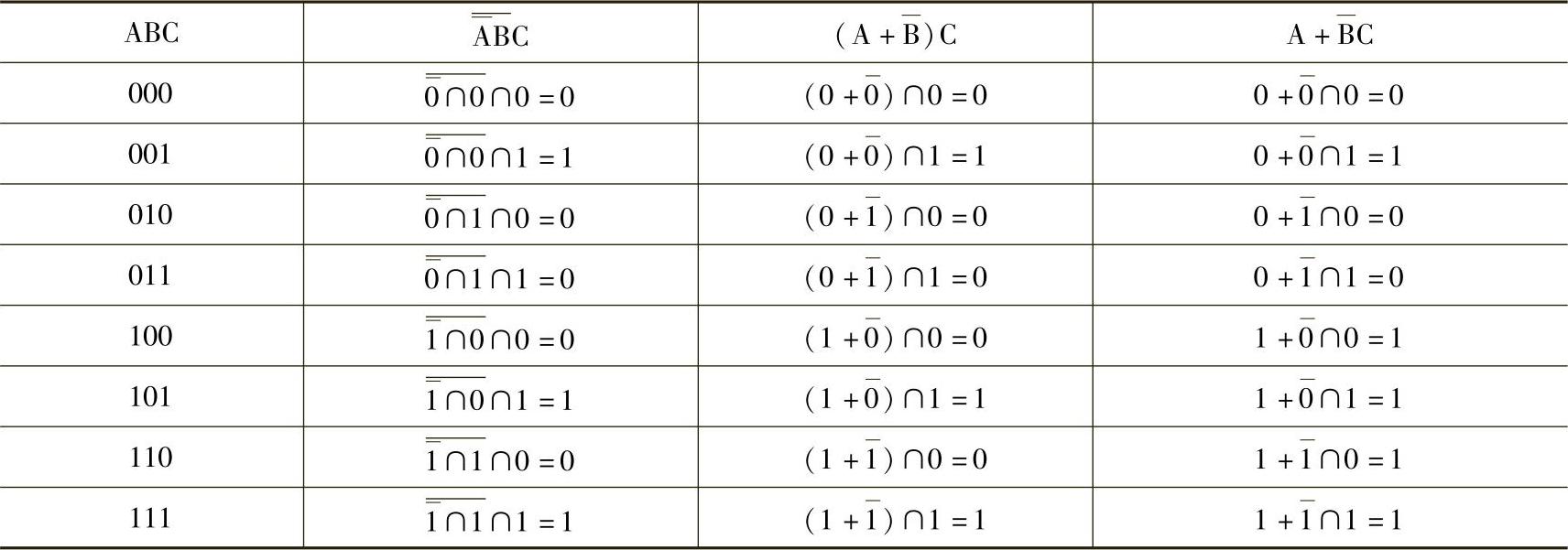
通过实际运算证明：

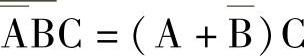
等效关系成立。

摩根定理说明，一个逻辑关系可有多种表达式形式，也就是可用多种逻辑电路实现，这就为制作实际数字电路提供了充分的选择余地。

3.按逻辑器件变换表达式的运算结构

表达式中的运算类型以及运算顺序是跟逻辑图的结构相对应的，不同的逻辑器件对应不同的逻辑运算符号。按指定的逻辑器件去设计逻辑电路，就要通过变换得出相应运算结构的表达式。

在逻辑代数中，常按运算类型（对应逻辑器件）和顺序给表达式命名，例如：与或式、与非—与非式、或与式、与或非式等。由于一片数字集成电路内含多个同类逻辑门，为充分利用电路资源，在实际制作电路时，通常选用同种逻辑器件构成，如与非门构成“与非—与非”结构、或非门构成的“或非—或非”结构。

【例4-3】下面是一个逻辑函数表达式的4种结构：

和上述4种表达式结构对应的逻辑图如图4-12所示。

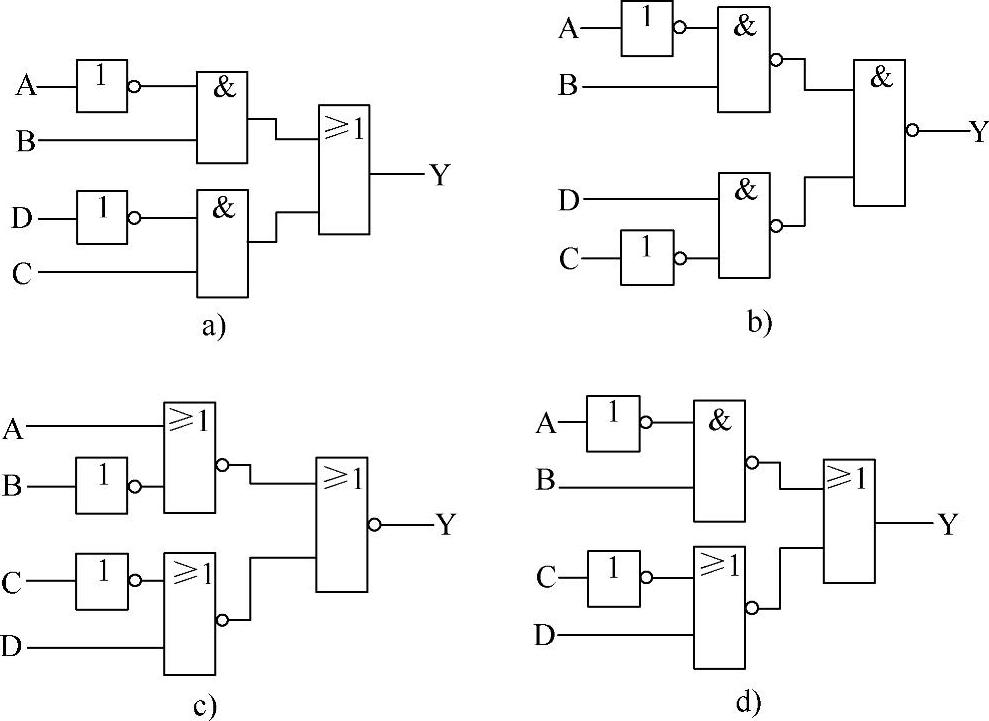
图4-12 例4-3的4种逻辑图